Question
Question: In the potentiometer circuit shown below, balancing length AJ when switch \(S_1\) is closed and \(S_...
In the potentiometer circuit shown below, balancing length AJ when switch S1 is closed and S2 is open Is found to be 60 cm and that (AJ’) when S2 is closed and S1 is open is 80 cm. The unknown resistance x then is
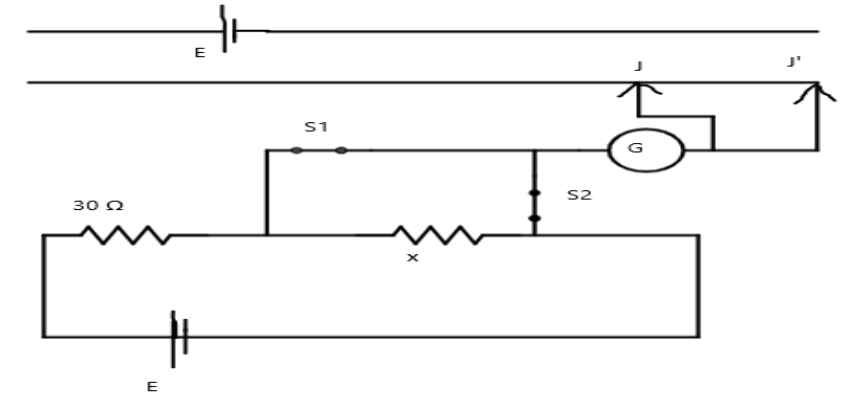
A) 5Ω
B) 15Ω
C) 10Ω
D) 20Ω
Solution
Consider a constant current that is flowing through a cross-section of area. It has the same composition and the potential drop across any length of the wire is directly proportional to the length. This is known as the principle of the potentiometer. The voltage developed in the circuit is directly proportional to the current and the resistance.
Formula used:
The emf of the cell or the potential drop of the cell, ε=kl1 when S1is closed and k is the potential gradient (mv).
The potential difference at the balance point,V=kl2when S2is closed and k is the potential gradient (mv).
From Ohm’s Law, V=IR, where R is the resistance.
Complete step by step solution:
Given details:
The position of the jockey in the first case, l1=80 cm
The position of the jockey in the second case,l2=60 cm
Given resistance, R=30Ω
Now we can use the above formulas to generate a relation between ε and V
Dividing the two equations, Vε=l2l1
Let X be the unknown resistance of the cell. If the current I flow through cell when it is shunted with resistance R, then from Ohm’s Law we get ε=I(R+x) and V=IR
Therefore, diving the equations we get,
Vε=RR+x=l2l1
⇒RR + x=l2l1
⇒1+Rx=l2l1
Taking the 1 to the right-hand side we get,
⇒Rx=l2l1−1
⇒x = R(l2l1−1)
Now using the values, we get the value ofX,
⇒x = 30(6080−1)
⇒x=30(68−1)
Dividing the terms, we get,
⇒x=30(34−1)
⇒x=30(31)
∴x=10Ω
The correct option is (C).
Note:
Emf of a cell: The electromotive force of a cell is the maximum potential difference between two electrodes of a cell.
2. A potentiometer is used to measure the potential difference in a circuit.
3. Potentiometer is used to measure very small potential differences.
4. It shows a significant balancing length for a small change in the potential difference is measured.
