Question

In the parabola ${{y}^{2}}=4ax$, the locus of middle points of all chords of constant length c is
$\begin{aligned} & \left( a \right)\left( 4ax-{{y}^{2}} \right)\left( {{y}^{2}}-4{{a}^{2}} \right)={{a}^{2}}{{c}^{2}} \\\ & \left( b \right)\left( 4ax+{{y}^{2}} \right)\left( {{y}^{2}}+4{{a}^{2}} \right)={{a}^{2}}{{c}^{2}} \\\ & \left( c \right)\left( 4ax+{{y}^{2}} \right)\left( {{y}^{2}}-4{{a}^{2}} \right)={{a}^{2}}{{c}^{2}} \\\ & \left( d \right)\left( 4ax-{{y}^{2}} \right)\left( {{y}^{2}}+4{{a}^{2}} \right)={{a}^{2}}{{c}^{2}} \\\ \end{aligned}$

Answer 1

Hint: To solve the question given above, we will consider that the points making the chords are $P\left( at_{1}^{2},2a{{t}_{1}} \right)\,and\ Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ according to the parametric form we will then consider that R (h, k) is the midpoint of P and Q. Then we will find h and k in terms of ${{a}_{1}},{{t}_{1}}\ and\text{ }{{t}_{2}}.$ Then we will find the distance between P and Q with the help of distance formula and we will equate it to c to get the locus.

Complete step-by-step answer:
The rough sketch of parabola as given in the question is drawn below:

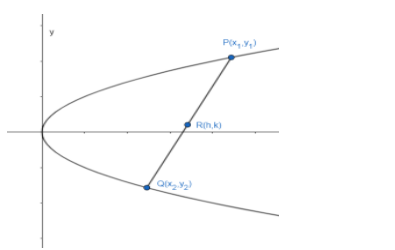
Let the chord of parabola be made by the points P and Q. We can also write ${{x}_{1}}\text{ }and\ {{y}_{1}}\ as\ a{{t}_{1}}\ and\ 2a{{t}_{1}}$ respectively according to the parametric form. Thus, we will get $P\left( at_{1}^{2},2a{{t}_{1}} \right)$. Similarly we can say that $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$. Now, have assumed that R (h, k) is the midpoint of P and Q. Now we will apply the midpoint formula. The midpoint (x, y) of G (a, b) and H (c, d) is given by the formula:
$\begin{aligned} & x=\dfrac{a+c}{2} \\\ & y=\dfrac{b+d}{2} \\\ \end{aligned}$
Thus, we will get:

& h=\dfrac{at_{1}^{2}+a{{t}^{2}}_{2}}{2} \\\ & \Rightarrow 2h=at_{1}^{2}+a{{t}^{2}}_{2} \\\ & \Rightarrow \dfrac{2h}{a}=t_{1}^{2}+{{t}^{2}}_{2}.........\left( 1 \right) \\\ \end{aligned}$$ Similarly, $$k=\dfrac{2a{{t}_{1}}+a{{t}_{2}}}{2}$$ $\begin{aligned} & \Rightarrow k=a{{t}_{1}}+a{{t}_{2}} \\\ & \Rightarrow \dfrac{k}{a}={{t}_{1}}+{{t}_{2}}..........\left( 2 \right) \\\ \end{aligned}$ Now, we will square the equation (2). Thus, we will get: ${{\left( \dfrac{k}{a} \right)}^{2}}={{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}$ Now, we will apply identity: ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2a{{b}^{2}}$ $$\begin{aligned} & \Rightarrow {{\left( \dfrac{k}{a} \right)}^{2}}=t_{1}^{2}+t_{2}^{2}+2{{t}_{1}}{{t}_{2}} \\\ & \Rightarrow \dfrac{{{k}^{2}}}{{{a}^{2}}}-2{{t}_{1}}{{t}_{2}}=t_{1}^{2}+t_{2}^{2}........\left( 3 \right) \\\ \end{aligned}$$ From (1) and (3), we have: $$\begin{aligned} & \Rightarrow \dfrac{{{k}^{2}}}{{{a}^{2}}}-2{{t}_{1}}{{t}_{2}}=\dfrac{2h}{a} \\\ & \Rightarrow 2{{t}_{1}}{{t}_{2}}=\dfrac{{{k}^{2}}}{{{a}^{2}}}-\dfrac{2h}{a} \\\ & \Rightarrow 2{{t}_{1}}{{t}_{2}}=\dfrac{{{k}^{2}}-2ah}{{{a}^{2}}} \\\ & \Rightarrow {{t}_{1}}{{t}_{2}}=\dfrac{{{k}^{2}}-2ah}{2{{a}^{2}}}...........\left( 4 \right) \\\ \end{aligned}$$ Now, we are given that the distance between P and Q is the distance between A (a,b) and B(c,d) is given by: $\left| AB \right|=\sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{^{2}}}}$ Thus, we have: $c=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$ On putting the parametric form of the variable ${{x}_{1}},{{x}_{2}},{{y}_{1}}\text{ }and\text{ }{{y}_{2}}$, we will get: $$\begin{aligned} & \Rightarrow c=\sqrt{{{\left( at_{1}^{2}-at_{2}^{2} \right)}^{2}}+{{\left( 2a{{t}_{1}}-2a{{t}_{2}} \right)}^{2}}} \\\ & \Rightarrow c=\sqrt{{{a}^{2}}{{\left( t_{1}^{2}-t_{2}^{2} \right)}^{2}}+{{a}^{2}}{{\left( 2{{t}_{1}}-2{{t}_{2}} \right)}^{2}}} \\\ & \Rightarrow c=a\sqrt{{{\left( t_{1}^{2}-t_{2}^{2} \right)}^{2}}+{{\left( 2{{t}_{1}}-2{{t}_{2}} \right)}^{2}}} \\\ \end{aligned}$$ Now, we will square both sides. Thus, we will get: $\Rightarrow \dfrac{{{c}^{2}}}{{{a}^{2}}}={{\left( t_{1}^{2}-t_{2}^{2} \right)}^{2}}+{{\left( 2{{t}_{1}}-2{{t}_{2}} \right)}^{2}}.$ Now, we will use the identity: ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right).$ Thus, we will get: $\Rightarrow \dfrac{{{c}^{2}}}{{{a}^{2}}}={{\left[ \left( {{t}_{1}}+{{t}_{2}} \right)\left( {{t}_{1}}-{{t}_{2}} \right) \right]}^{2}}+4\left[ {{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}} \right]$ Now, taking ${{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}$ common from the right hand side. Thus, we will get: $\Rightarrow \dfrac{{{c}^{2}}}{{{a}^{2}}}={{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}\left[ {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+4 \right]$ Now, we will apply identity: ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab.$ Thus, we will get: $\Rightarrow \dfrac{{{c}^{2}}}{{{a}^{2}}}=\left[ t_{1}^{2}+t_{2}^{2}+2{{t}_{1}}{{t}_{2}} \right]\left[ {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+4 \right]..........\left( 5 \right)$ Now, we will put the values of $$\left( t_{1}^{2}+t_{2}^{2} \right),\left( {{t}_{1}}{{t}_{2}} \right)\text{ }and\ \left( {{t}_{1}}+{{t}_{2}} \right)$$ from (1),(4) and (2) respectively into (5). Thus, after doing this, we will get: $\begin{aligned} & \Rightarrow \dfrac{{{c}^{2}}}{{{a}^{2}}}=\left[ \dfrac{2h}{a}-2\left( \dfrac{{{k}^{2}}-2ah}{2{{a}^{2}}} \right) \right]\left[ \dfrac{{{k}^{2}}}{{{a}^{2}}}+4 \right] \\\ & \Rightarrow \dfrac{{{c}^{2}}}{{{a}^{2}}}=\left[ \dfrac{2ha-{{k}^{2}}+2ah}{{{a}^{2}}} \right]\left[ \dfrac{{{k}^{2}}+4{{a}^{2}}}{{{a}^{2}}} \right] \\\ & \Rightarrow \dfrac{{{c}^{2}}}{{{a}^{2}}}=\left[ \dfrac{\left( 4ah-{{k}^{2}} \right)\left( {{k}^{2}}+4{{a}^{2}} \right)}{{{a}^{2}}\times {{a}^{2}}} \right] \\\ & \Rightarrow {{a}^{2}}{{c}^{2}}=\left( 4ah-{{k}^{2}} \right)\left( {{k}^{2}}+4{{a}^{2}} \right) \\\ \end{aligned}$ On putting x in place of h and y in place of k, we will get: $\left( 4ax-{{y}^{2}} \right)\left( {{y}^{2}}+4{{a}^{2}} \right)={{a}^{2}}{{c}^{2}}$ Hence option (d) is correct. Note: Instead of taking the points on the chord as the parametric form of points, we can also take points as shown. The equation of parabola is: ${{y}^{2}}=4ax.$ The points P and Q will satisfy it. Thus, ${{y}^{2}}=4a{{x}_{1}}\Rightarrow {{x}_{1}}=\dfrac{y_{1}^{2}}{4{{a}_{1}}}$ Similarly ${{x}_{2}}=\dfrac{y_{2}^{2}}{4{{a}_{2}}}$ Now, $$h=\dfrac{\dfrac{y_{1}^{2}}{4{{a}_{1}}}+\dfrac{y_{2}^{2}}{4{{a}_{2}}}}{2}$$ $\Rightarrow 8{{a}_{1}}h=y_{1}^{2}+y_{2}^{2}.........\left( 1 \right)$ Similarly, $$k=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$$ $\Rightarrow 2k={{y}_{1}}+{{y}_{2}}........\left( 2 \right)$ When we will put these values in the distance formula and equate it to c, we will get the same result.