Question

In the network shown, points A, B and C are at potentials of 70 V, zero and 10 V respectively. Then

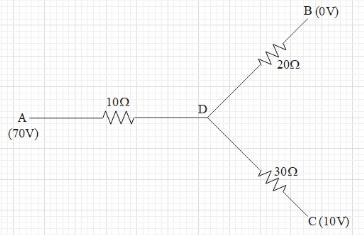
A. Point D is at a potential of 40V.
B. The currents in the sections AD, DB, DC are in the ratio 3 : 2 : 1
C. The currents in the sections AD, DB, DC are in the ratio 1 : 2 : 3
D. The network draws a total power of 200 W.

Answer 1

Use Ohm’s law write down the equation for the potential difference across each resistance. Also use the junction law to help further. Form four different equations to find the value of potential at point D and the currents in the three sections.

Formula used:
$\Delta V=iR$
$P={{i}^{2}}R$
where $i$ is the current in the resistance and $\Delta V$ is the potential difference across the resistance.

Complete step by step answer:
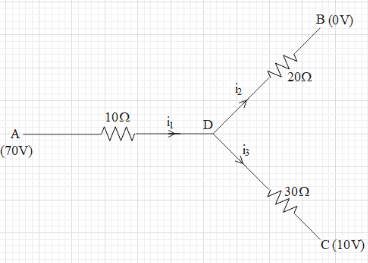
Let the currents in the sections AD, DB and DC be ${{i}_{1}}$, ${{i}_{2}}$ and ${{i}_{3}}$ respectively, as shown in the figure below.

From this we know that the potential difference (or voltage) across a resistance R is equal to the product of the resistance and the current flowing in the resistance i.e. $\Delta V=iR$, where i is the current in the resistance and $\Delta V$ is the potential difference across the resistance.
Therefore, we can write that
${{V}_{A}}-{{V}_{D}}={{i}_{1}}{{R}_{1}}$ ….. (i)
$\Rightarrow{{V}_{D}}-{{V}_{B}}={{i}_{2}}{{R}_{2}}$ ….. (ii)
$\Rightarrow{{V}_{D}}-{{V}_{C}}={{i}_{3}}{{R}_{3}}$ ….. (iii)
It is given that ${{V}_{A}}=70V$, ${{V}_{B}}=0V$, ${{V}_{C}}=10V$.
And
${{R}_{1}}=10V$, ${{R}_{2}}=20V$, ${{R}_{3}}=30V$.
Substitute the values in (i), (ii) and (iii).
$70-{{V}_{D}}=10{{i}_{1}}$ ….. (iv)
$\Rightarrow {{V}_{D}}-0=20{{i}_{2}}$ ….. (v)
$\Rightarrow {{V}_{D}}-10=30{{i}_{3}}$ ….. (vi)

Now, from junction low, we get that ${{i}_{1}}={{i}_{2}}+{{i}_{3}}$ ….. (vii).
Subtract (vi) from (v).
$\Rightarrow {{V}_{D}}-\left( {{V}_{D}}-10 \right)=20{{i}_{2}}-30{{i}_{3}}$
$\Rightarrow 10=20{{i}_{2}}-30{{i}_{3}}$
$\Rightarrow 2{{i}_{2}}-3{{i}_{3}}=1$ …. (viii).
Now add (iv) and (v).
$\Rightarrow 70-{{V}_{D}}+{{V}_{D}}=10{{i}_{1}}+20{{i}_{2}}$
$\Rightarrow {{i}_{1}}+2{{i}_{2}}=7$ ….. (ix)
Substitute the value of ${{i}_{1}}$ from (vii) in (ix).
$\left( {{i}_{2}}+{{i}_{3}} \right)+2{{i}_{2}}=7$
$\Rightarrow 3{{i}_{2}}+{{i}_{3}}=7$ …. (x)
On solving (x) and (viii) we get that ${{i}_{2}}=2A$ and ${{i}_{3}}=1A$.
This means that ${{i}_{1}}={{i}_{2}}+{{i}_{3}}=2+1=3A$.
Therefore, the currents in the sections AD, DB, DC are in the ratio ${{i}_{1}}:{{i}_{2}}:{{i}_{3}}$, which is equal to 3 : 2 : 1.
Now, substitute the value of ${{i}_{2}}$ in (v).
${{V}_{D}}=20(2)=40V$
This means that the potential at point D is 40V.
The power dissipated through a resistance R, carrying current i is equal to $P={{i}^{2}}R$.
Therefore, we can write that
${{P}_{1}}=i_{1}^{2}{{R}_{1}}$
$\Rightarrow{{P}_{2}}=i_{2}^{2}{{R}_{2}}$
$\Rightarrow{{P}_{3}}=i_{3}^{2}{{R}_{3}}$
Substitute the known values.
$\Rightarrow {{P}_{1}}={{(3)}^{2}}(10)=90W$
$\Rightarrow{{P}_{2}}={{(2)}^{2}}(20)=80W$
$\Rightarrow{{P}_{3}}={{(1)}^{2}}(30)=30W$.
The total power drawn by the given circuit is,
$\therefore P={{P}_{1}}+{{P}_{2}}+{{P}_{2}}=90+80+30=200W$

Hence, the correct options are (A), (B) and (D).

Note: To find the total power of a given circuit, we can also calculate the effective resistance (${{\operatorname{R}}_{eff}}$) of the circuit. Then the total power dissipated by the circuit is equal to $P={{i}^{2}}{{\operatorname{R}}_{eff}}$. Here, $i$ is the main current in the circuit. However, we can calculate the effective resistance of a circuit and so have to find the power drawn by individual resistance.