Question
Question: In the network shown in figure, each resistance is\(\; R\). The equivalent resistance between A and ...
In the network shown in figure, each resistance isR. The equivalent resistance between A and B is:
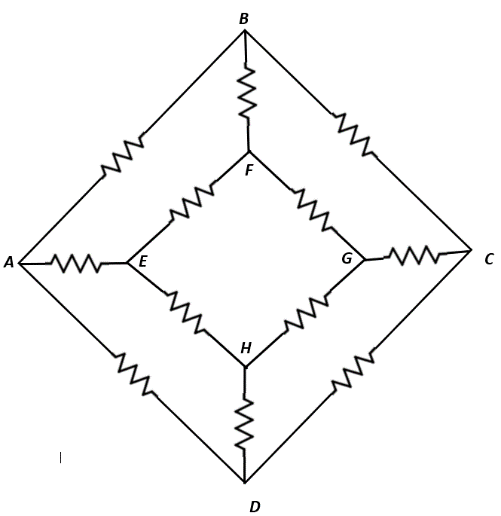
A. 43R
B. 65R
C. 127R
D. 34R
Solution
Begin by construing that a battery is connected across the terminals A and B. Then determine the points that possess the same voltage. The resistors across these points will be parallel to each other. Remember that resistances connected in series are additive whereas those in parallel have an equivalent resistance less than their individual resistances. Use this to calculate the effective resistance of the inner and outer loops, following which you can arrange the resultant equivalent circuit across the terminals A and B and calculate the equivalent resistance.
Formula used:
Effective resistance of two resistors in series: Reff=R1+R2
Effective resistance of two resistors in parallel: Reff1=R11+R21
Complete step-by-step answer:
To find the equivalent resistance between A and B, let us assume a battery is connected across A and B.
When this is done, same voltage flows through branches BF and BC, which means that RBF∣∣RBC, therefore, the equivalent resistance between B, F and C will be:
RB↔F,C=RBF+RBCRBFRBC=R+RR×R=2R
Similarly, same voltage flows through branches AE and AD, which means that RAD∣∣RAE, therefore, the equivalent resistance between A, E and D will be:
RA↔E,D=RAE+RADRAERAD=R+RR×R=2R
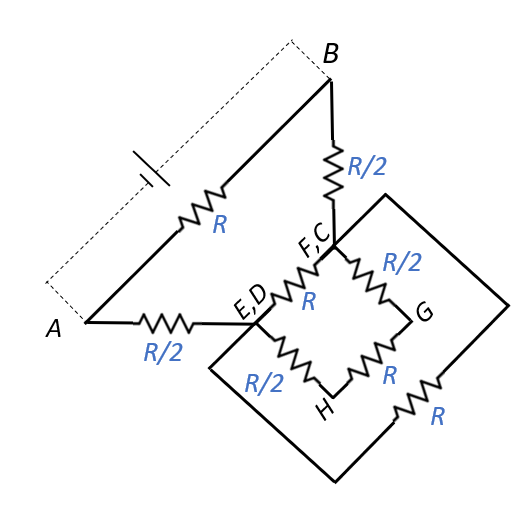
Now, at G, RGF∣∣RGC, therefore, the equivalent resistance between G, F and C will be:
RG↔F,C=RGF+RGCRGFRGC=R+RR×R=2R
Similarly, at H, RHE∣∣RHD, therefore, the equivalent resistance between H, E and D will be:
RH↔E,D=RHE+RHDRHERHD=R+RR×R=2R
If REF=R=RGH, then the equivalent resistance on the inner loop EFGH will be:
REFGH=REF∣∣(RG↔F,C+RGH+RH↔E,D)=R∣∣(2R+R+2R)=R∣∣2R
⇒REFGH=R+2RR×2R=32R
Now, REFGH is in parallel with RCD=R, therefore, the equivalent resistance will be:
R′=REFGH+RCDREFGHRCD=(32R+R)(32R×R)=(35R)(32R2)=52R
Now we can find the equivalent resistance across terminals A and B as follows:
Req=RAB∣∣(RB↔F,C+R′+RA↔E,D)
⇒Req=R∣∣(2R+52R+2R)
⇒Req=R∣∣(105R+4R+5R)=R∣∣1014R=R∣∣57R
Therefore, Req=(R+57R)(R×57R)=57R2×12R5=127R
So, the correct answer is “Option C”.
Note: Remember that a series circuit is a voltage divider whereas a parallel circuit is a current divider. We add up all the resistances in a series circuit because the resistances are arranged in such a way that the current has only one path to take. However, when resistances are connected in parallel, there are multiple paths for the current to pass through but have the same potential difference across them. This results in a net resistance that is lower than any of the individual resistances.
