Question
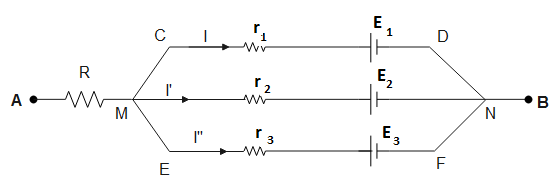
Question: In the network shown, find the potential difference between A and B. (\(R={{r}_{1}}={{r}_{2}}={{r}...
In the network shown, find the potential difference between A and B.
(R=r1=r2=r3=1Ω,E1=E2=E3=1V)
Solution
The circuit has three branches. Since they are in parallel combination; the potential drop in each branch is equal. Ohm’s law gives us the relationship between the current, potential drop and resistance in a circuit. Using ohm’s law and Kirchhoff’s fundamental laws for circuit analysis, we can solve the given circuit.
Formulas used:
R=IV
Complete step by step solution:
The ohm’s law gives the relationship between resistance, current and potential difference in a circuit. It is given as-
R=IV …………………. (1)
Here, R is the resistance
V is the potential difference
I is current
Given, a circuit between two points A and B consists of three branches each with a battery and a resistor. Since the branches are connected in parallel, the potential drop on each branch will be equal.

Let the current through the branch CD be I
From eq (1), the value of I will be-
I=RV⇒I=13=3A
Let the current through the branch MN be I′
From eq (1), the value of I′ will be-
I′=12=2A
Let the current in branch EF be I′′
From eq (1), the value of I′′ will be-
I′′=11=1A
Let the current flowing through resistance,R be I1
By Kirchhoff’s current law, the value of I1 is,
I1=I+I′+I′′⇒I1=3+2+1∴I1=6A
By Kirchhoff’s voltage law, applying loop in AMCDNB
VA−I1R−I×1−3=VB⇒VB−VA=−6×1−3×1−3VB−VA=−12V∴VA−VB=12V
In the circuit between A and B, the potential difference is 12V.
Additional Information:
The Kirchhoff’s current law states that the total charge passing through a junction is conserved. This means, the sum of incoming charges is equal to the sum of outgoing charges. Kirchhoff's voltage law states that the algebraic sum of all the potential drops in a loop is equal to zero. This is because the loop is a closed conducting path, so no energy loss takes place.
Note:
Just like resistors or capacitors, batteries can also be connected in combinations in a circuit. The two possible combinations are series and parallel. In a series combination of batteries, the equivalent voltage is the sum of voltages of all batteries while in parallel combination, the ratio of equivalent voltage and equivalent resistance is the sum of ratios of voltages and resistances.
