Question

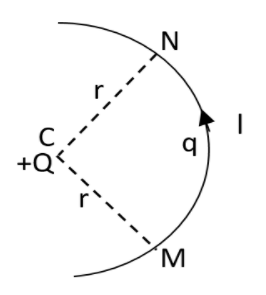
In the mentioned diagram, a charge $Q$ is fixed. Another charge $q$ is found to be moving along a circular arc $MN$ of radius $r$ around it, from the point $M$ to the point $N$ such that the length of the arc $MN=l$. Calculate the work done in this process?

$\begin{aligned} & A.zero \\\ & B.\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Qq}{{{r}^{2}}}l \\\ & C.\dfrac{Qq}{2{{\varepsilon }_{0}}{{r}^{2}}}l \\\ & D.\dfrac{Qq}{2\pi {{\varepsilon }_{0}}{{r}^{2}}} \\\ \end{aligned}$

Answer 1

First of all let us analyse the diagram. As we can see that the point $M$ and $N$ are at identical distances from point $Q$. Therefore these will be having identical potential. The potential of a point can be found by taking the product of the ratio of one to the $4\pi {{\varepsilon }_{0}}$ and the ratio of the charge at this point to the square of the distance between them. The work done at this point can be found by taking the product of the potential at the point to the charge at the point. This will help you in answering this question.

Complete answer:
First of all let us analyse the diagram. As we can see that the point $M$ and $N$ are at identical distances from point $Q$. Therefore these will be having identical potential.
The potential of a point can be found by taking the product of the ratio of one to the $4\pi {{\varepsilon }_{0}}$ and the ratio of the charge at this point to the square of the distance between them. As the potentials are equal, we can write that,
${{V}_{M}}={{V}_{N}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{q}{r}$
As they are equal their difference will be equivalent to zero. That is,
${{V}_{M}}-{{V}_{N}}=0$
The work done at this point can be found by taking the product of the potential at the point to the charge at the point. This can be written as,
$W=\left( {{V}_{M}}-{{V}_{N}} \right)q$
Substituting the values in the equation will give,
$W=\left( {{V}_{M}}-{{V}_{N}} \right)q=0\times q=0$

Therefore the correct answer has been obtained as option A.

Note:
An electric potential is also known as the electric field potential or electrostatic potential. It is defined as the amount of work required to move a unit of electric charge from a reference position to a particular location in an electric field without creating an acceleration. Generally the reference point has been taken as the earth or infinity.