Question
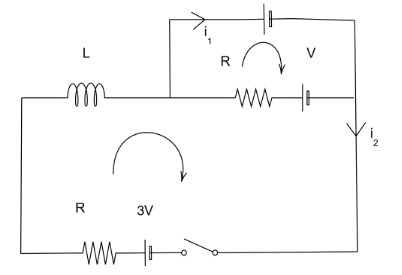
Question: In the LR circuit shown, what is the variation of the current \( I \) as a function of time? The swi...
In the LR circuit shown, what is the variation of the current I as a function of time? The switch is closed at time t=0s
Solution
We start by noting down the given data. Then we apply Kirchhoff's voltage law and find the value of current and the relationship between the current, voltage and resistance. Using the circuit as two separate loops we get a value for the value of individual currents in the loops. We find the resultant of the two to find the value of total current.
Complete Step By Step Answer:
We start by writing down the given information. We then find the relationship between the individual currents in the loops.
Let us consider I=i1+i2
Where, i1 is the current travelling through the small loop
i2 is the current travelling through the bigger loop
Taking the Kirchhoff’s law in the first loop, i1R+2V−V=0
Now we take the unknown value of current on one side and the known value on the other. This helps us to get the value as, i1=R−V
In the second or the bigger loop, we apply the Kirchhoff’s law we get i2R+Ldtdi2−i1R+V−3V=0
Substitute the value of current through loop one and get, (I+RV)R+LdtdI+V+V−3V=0
LdtdI=−IR
We take the known values to the other side and get
dtdI=L−IR
Now we will integrate this value. Before we integrate this equation, we can see that the value of current that is unknown is on both sides, so we bring it to one side and then integrate.
∫IdI=∫2−Rdt
Solving this, we get ln(R−V)I=2−Rdt
To remove the value of natural logarithm, we take base e on both the sides and get,
I=R−Ve(2−Rt)
The variation of current is given by, I=R−Ve(2−Rt)
Note:
A resistor–inductor circuit, or RL filter or RL network, is an electrical circuit that consists of resistors and inductors which are driven by a voltage or current source. A RL circuit consisting of one resistor and one inductor is called a first degree RL Circuit. The kirchhoff's loop rule helps us to form the equations for the voltage drops in the loops.
