Question

In the Kundts tube experiment (shown in fig. (i)), the rod is clamped at the end instead of clamping it at the center as shown in fig. (ii). It is known that speed of sound in air is 330 m/s, powder piles up at successive distance of 0.6 m and length of rod used is 1m, speed of sound in rod is

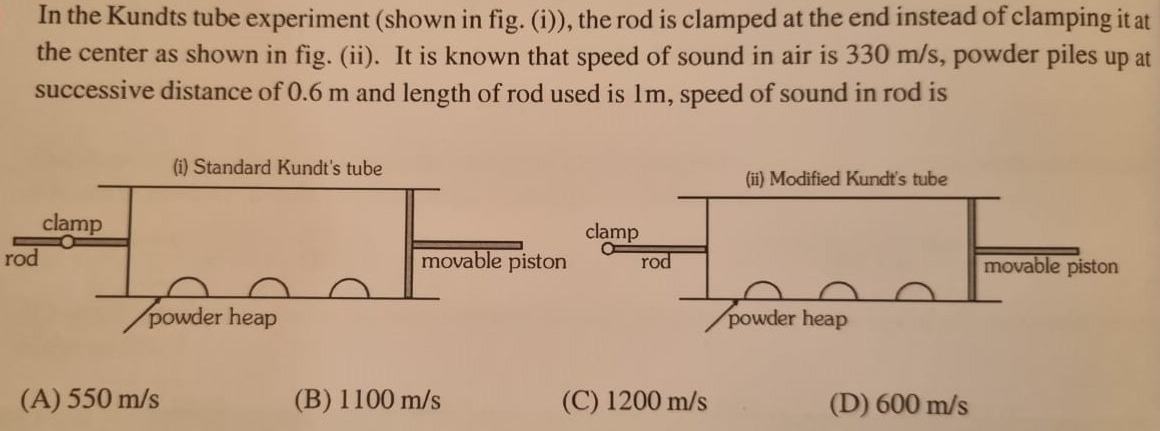
• A. 550 m/s
• B. 1100 m/s
• C. 1200 m/s
• D. 600 m/s

Answer 1

Answer: (B)

1100 m/s

Answer 2

Here's how to determine the speed of sound in the rod:

1. Wavelength in air: The distance between successive powder heaps is half the wavelength of sound in air. Therefore, $\lambda_{air} = 2 \times 0.6 \, \text{m} = 1.2 \, \text{m}$.

2. Frequency of sound in air: Using the formula $v = f\lambda$, we find the frequency: $f = \frac{v_{air}}{\lambda_{air}} = \frac{330 \, \text{m/s}}{1.2 \, \text{m}} = 275 \, \text{Hz}$.

3. Frequency of the rod: The frequency of vibration of the rod is equal to the frequency of the sound in the air, so $f = 275 \, \text{Hz}$.

4. Wavelength in the rod: For a rod clamped at one end, the fundamental mode has a wavelength four times the length of the rod: $\lambda_{rod} = 4 \times L_{rod} = 4 \times 1 \, \text{m} = 4 \, \text{m}$.

5. Speed of sound in the rod: Finally, calculate the speed of sound in the rod: $v_{rod} = f \lambda_{rod} = 275 \, \text{Hz} \times 4 \, \text{m} = 1100 \, \text{m/s}$.