Question

In the interval $\left[ 0,3 \right]$ , the number of points at which the function $\left[ {{x}^{2}} \right]\sin \pi x$ ( $\left[ . \right]$ is the usual integral part) is discontinuous are:
(a)$4$
(b)$5$
(c) $6$
(d) $8$

Answer 1

Hint: $\left[ g\left( x \right) \right]$ is continuous only at those points at which $g\left( x \right)$ does not attain an integer value . If $g\left( x \right)$ attains an integer value , $\left[ g\left( x \right) \right]$ becomes discontinuous .

Complete step-by-step solution -
Let the given function be $f\left( x \right)$ . So, we can say $f\left( x \right)=\left[ {{x}^{2}} \right]\sin \pi x$ .
Now , we know the greatest integer function is defined as a function which rounds down a real number to the nearest integer . Its graph is as given as

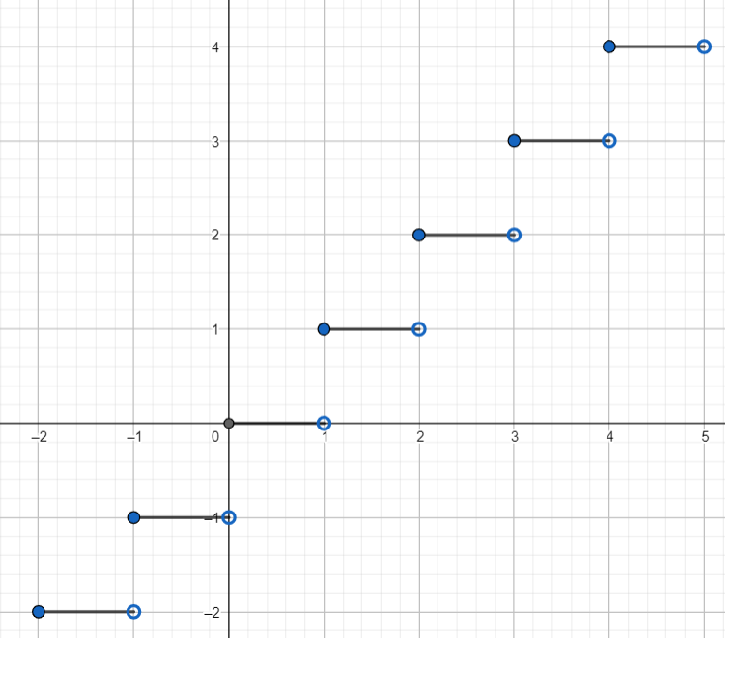
From the graph , we can clearly see that the graph is in the form of steps . So , from the graph we can conclude that the greatest integer function is discontinuous at integer points .
Now , we can define the function $\left[ {{x}^{2}} \right]$ as:

& 0,\text{ }0\le x<1 \\\ & 1,\text{ }1\le x<\sqrt{2} \\\ & 2,\text{ }\sqrt{2}\le x<\sqrt{3} \\\ & 3,\text{ }\sqrt{3}\le x<2 \\\ & 4,\text{ }2\le x<\sqrt{5} \\\ & 5,\text{ }\sqrt{5}\le x<\sqrt{6} \\\ & 6,\text{ }\sqrt{6}\le x<\sqrt{7} \\\ & 7,\text{ }\sqrt{7}\le x\sqrt{8} \\\ & 8,\text{ }\sqrt{8}\le x<3 \\\ & 9,\text{ }x=3 \\\ \end{aligned} \right.$$ The graph of the function $$\left[ {{x}^{2}} \right]$$ is given as:  From the graph we can see that $$\left[ g\left( x \right) \right]$$ is discontinuous at points where $$g\left( x \right)$$ becomes an integer. So , $$\left[ {{x}^{2}} \right]$$ should be discontinuous at $$x=0,x=1,x=\sqrt{2},x=\sqrt{3},x=2,x=\sqrt{5},x=\sqrt{6},x=\sqrt{7},x=\sqrt{8}$$ and $$x=3$$ . But , since $$f\left( x \right)$$ is defined in the interval $$x\in \left[ 0,3 \right]$$ , $$f\left( x \right)$$ does not exist to the left of $$x=0$$ and to right of $$x=3$$ . So , continuity of function $$f\left( x \right)$$ cannot be discussed at $$x=0$$ and at $$x=3$$ . Now , in the interval $$\left[ 0,3 \right]$$ , we can see there are $$8$$ points at which $$\left[ {{x}^{2}} \right]$$ is discontinuous i.e. $${{x}^{2}}$$ attains an integer value. These points are $$x=1,\text{ }x=\sqrt{2},\text{ }x=\sqrt{3},\text{ }x=2,\text{ }x=\sqrt{5},\text{ }x=\sqrt{6},\text{ }x=\sqrt{7}$$ and $$x=\sqrt{8}$$ . Hence, the function $$f\left( x \right)=\left[ {{x}^{2}} \right]\sin \pi x$$ is discontinuous at these $$8$$ points. Note: The critical points for the function $$\left[ {{x}^{2}} \right]$$are $$x=0,x=1,x=\sqrt{2},x=\sqrt{3},x=2,x=\sqrt{5},x=\sqrt{6},x=\sqrt{7},x=\sqrt{8}$$ and $$x=3$$ and not $$x=0,x=1,x=2,x=3,x=4,x=5,x=6,x=7,x=8$$ and $$x=9$$ as in GIF there is square of x so the domain will contains those value whose square is an integer. Students often make this mistake. Due to such mistakes , they end up getting a wrong answer . So , such mistakes should be avoided .