Question

In the graph between $\sqrt v$ and $Z$ for the Mosley’s equation $\sqrt v = a(Z - b)$ , the intercept $OX$ is $- 1$ on $\sqrt v$ axis. What if the frequency when atomic number $(Z)$ is $51$ ?

(a) $50{s^{ - 1}}$
(b) $100{s^{ - 1}}$
(c) $2500{s^{ - 1}}$
(d) None of this

Answer 1

Atomic number can be defined as the total number of protons or the total number of electrons present in the atoms in their isolated neutral condition. It can also be represented as $Z$. For a neutral atom, the number of electrons in the atom is equal to the atomic number.
Formula used:
Mosley’s equation,
$\sqrt v = a(Z - b)$
Where, $v$ is frequency, $Z$ is atomic number, $a$ and $b$ are some constants.
Straight line formula,
$y = mx + c$
Where, $m$ is slope and $c$ is a constant.
Slope of a line, $m = \tan \theta$ , where $\theta$ is the angle with the $x -$ intercept.

Complete answer:

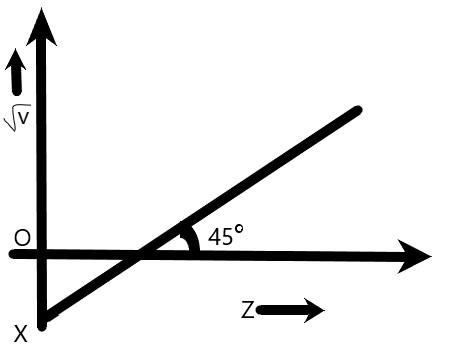
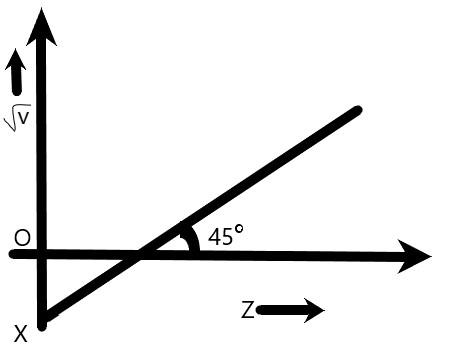
In these questions, given the intercept $OX$ is $- 1$ on $\sqrt v$ axis and from the graph shown that the angle between the line and the $x -$ intercept is $45^\circ$ .
Hence, Slope of the line, $m = \tan \theta$ , where $\theta$ is the angle between the straight line with the $x -$ intercept.
$m = \tan 45^\circ = 1$
Hence, line of the equation from the graph as follows,
$y = mx + c = x - 1$
Where, $m$ is slope and $c$ is a constant.
Expanding the Mosley’s equation,
$\sqrt v = a(Z - b) = aZ - ab$
Now, equating the Moseley’s equation with the line of the equation from the given graph, here, $\sqrt v$ is $y -$ intercept and $Z$ is $x -$ intercept.
Hence, $m = a = 1,c = - ab = - 1$
From the above,
$a = b = 1$
Hence, the Mosley’s equation becomes $\sqrt v = (Z - 1)$ , where, $v$ is frequency and $Z$ is atomic number,
Now, we have to find the frequency when atomic number $(Z)$ is $51$
Putting the value of $Z = 51$ in the Mosley’s equation $\sqrt v = (Z - 1)$
$\sqrt v = (51 - 1) = 50$
$\Rightarrow v = {\left( {50} \right)^2} = 2500{s^{ - 1}}$
Hence, the frequency is $2500{s^{ - 1}}$ when atomic number $(Z)$ is $51$ .

Hence, the correct option is (c) $2500{s^{ - 1}}$ .

Note:
Mass number can be defined as the sum of the total numbers of the protons and the number of neutrons present in the nucleus of the atom.