Question

In the given velocity-time graph, the net displacement of the object in time interval 0 to 8s is

A. 20m
B. 40m
C. -20m
D. Zero

Answer 1

elocity-time graph tracks the velocity of an object with respect to time. Velocity is the Displacement per unit time. So, to find displacement from the velocity time graph we need to calculate the area under the Velocity Time graph. The Net Displacement of the body from its position at t=0 can be calculated by calculating the total area under the velocity time graph.

Formula used:
We will use a simple formula to calculate the area of a rectangle.
$Area=length\times base$

Complete answer:
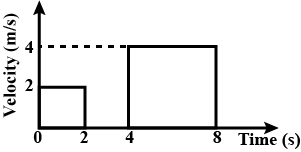
Let us start by getting a basic idea of the body in motion from the diagram. As we gather from the diagram the body started its motion with some velocity at time t=0 and came to a stop at time t=2, again the body started to move at t=4 and finally came to rest at t=8 second.
As mentioned in the hint the net displacement can be found out by calculating the total area under the velocity-time graph.

So in the given diagram, there are two squares, the first one is from t=0 to t=2, so the base is 2 and the velocity is constant at 2 so the length is also 2. So,

& Area=length\times base \\\ & Area=2\times 2 \\\ & Area=4 \\\ \end{aligned}$$ Similarly, for the second square length as well as the base is 4 $$\begin{aligned} & Area=length\times base \\\ & Area=4\times 4 \\\ & Area=16 \\\ \end{aligned}$$ Now, net displacement is the total area. So, $$\begin{aligned} & Net Displacement=TotalArea \\\ & Net Displacement=4+16 \\\ & Net Displacement=20 \\\ \end{aligned}$$ So, the Net Displacement of the object is 20m. **So, the correct answer is “Option A”.** **Note:** Area under the curve can be really useful in calculating quantities directly. It gives the product of the quantities at the axes. In the velocity-time graphs, the area gives the net displacement. In the acceleration-time graph, it gives velocity and so on.