Question

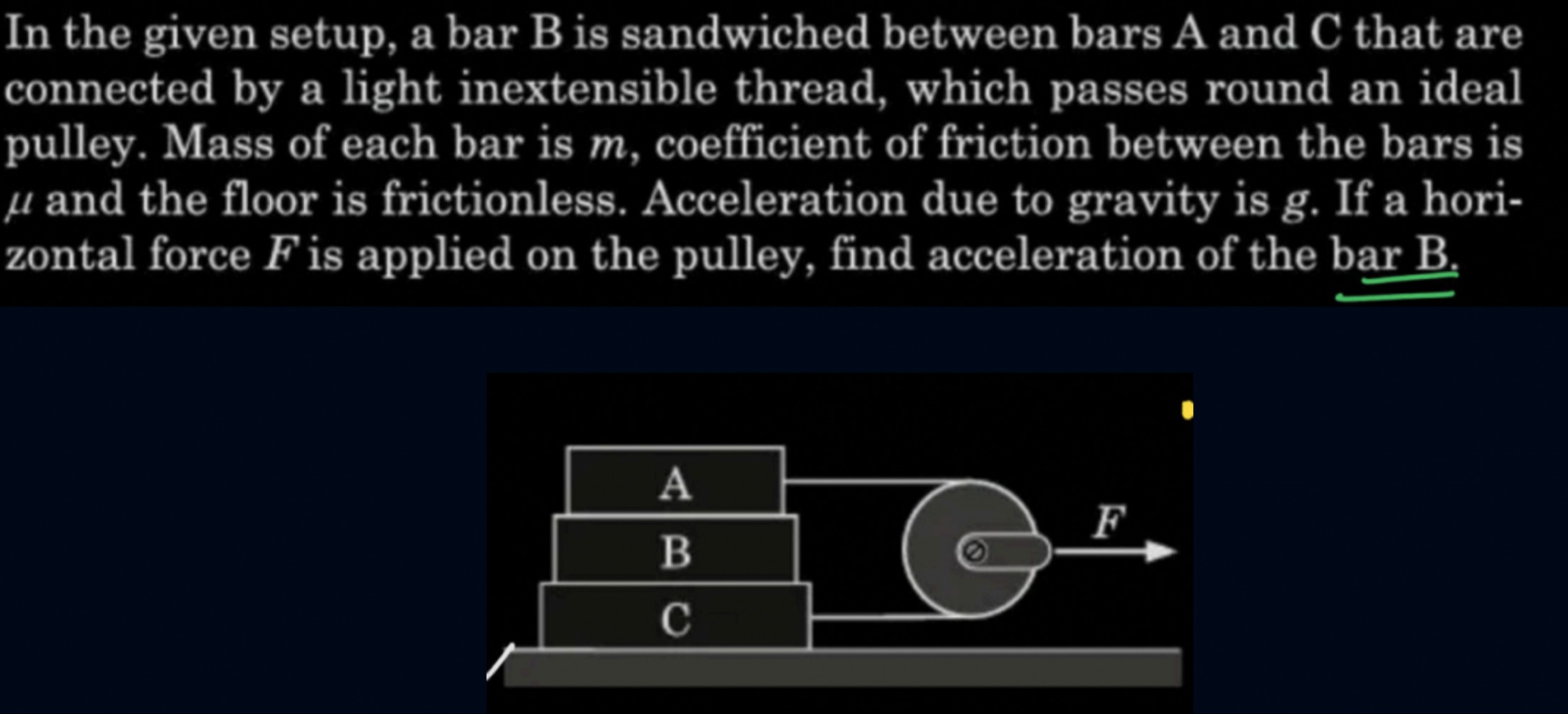
In the given setup, a bar B is sandwiched between bars A and C that are connected by a light inextensible thread, which passes round an ideal pulley. Mass of each bar is $m$, coefficient of friction between the bars is $\mu$ and the floor is frictionless. Acceleration due to gravity is $g$. If a horizontal force $F$ is applied on the pulley, find acceleration of the bar B.

Answer 1

3μg

Answer 2

To determine the acceleration of bar B, we need to analyze the forces acting on each bar and apply Newton's second law.

Let $m$ be the mass of each bar (A, B, C).
Let $\mu$ be the coefficient of friction between the bars.
The floor is frictionless.
The thread is light and inextensible, and the pulley is ideal (massless and frictionless).

If A moves faster than B ($a_A > a_B$), $f_{AB} = \mu N_{AB} = \mu mg$ (to the right).
If C moves faster than B ($a_C > a_B$), $f_{CB} = \mu N_{CB} = \mu (2mg)$ (to the right).
Then the net force on B is $F_B = f_{AB} + f_{CB} = \mu mg + 2\mu mg = 3\mu mg$.
So, $m a_B = 3\mu mg \implies a_B = 3\mu g$.

Therefore, the acceleration of bar B is $3\mu g$.

Note: The problem, as stated, leads to a contradiction if all standard assumptions (ideal pulley, inextensible string, constant $\mu$) are maintained. If $a_A=a_C$ is strictly enforced, then for $\mu \ne 0$, the system cannot move with both surfaces slipping. This would imply that the setup is not physically possible or that additional constraints are needed.