Question

In the given potentiometer circuit length of the wire $AB$ is $3m$ and resistance is $R = 4.5{\text{ }}\Omega$ . The length $AC$ for no deflection in galvanometer is

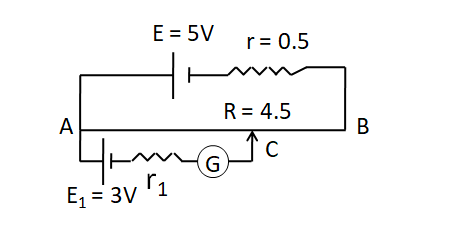
(A) $2m$
(B) $1.8m$
(C) $2.5m$
(D) $5.4m$

Answer 1

Hint To solve this question, we need to balance the potential between the upper and the lower branch of the circuit across the wire $AC$ . For this we need to find out the resistance of the wire $AC$ in terms of its length. After putting it in the equation of emf balance, the length would be obtained.

Complete step by step answer
Let the length of the wire $AC$ be $x{\text{ }}m$
Wire $AB$ is of length $3m$ and has a resistance of $R = 4.5{\text{ }}\Omega$ .
So, resistance of the wire $AC$ of length of length $x{\text{ }}m$ $= \dfrac{R}{3}\left( x \right)$
Or ${R_{AC}}$ $= \dfrac{{4.5}}{3}\left( x \right)$
$\Rightarrow {R_{AC}} = 1.5x$

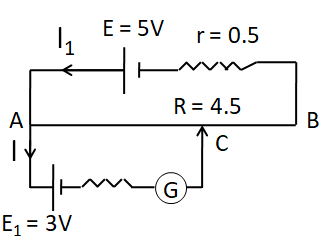
From the circuit given, the potential difference between $A$ and $C$
$\Rightarrow {V_{AC}} = {E_1} - I({r_1})$ … (1)
For no deflection in the galvanometer, the current in the lower branch of the circuit containing the galvanometer should be 0.
$\therefore$ Substituting $I = 0$ in the (1), we get
$\Rightarrow {V_{AC}} = {E_1} - 0({r_1})$
$\Rightarrow {V_{AC}} = {E_1}$
According to the circuit, ${E_1} = 3V$
$\therefore$ ${V_{AC}} = 3V$ … (2)
Now, the current ${I_1} = \dfrac{{{\text{Net emf}}}}{{{\text{Total Resistance}}}}$
$\Rightarrow {\text{Net emf = 5V}}$
$\Rightarrow {\text{Total Resistance = R + r}}$
According to question $R = 4.5{\text{ }}\Omega$ and ${\text{r = 0}}{\text{.5}}\Omega$
$\therefore {\text{Total Resistance = 4}}{\text{.5 + 0}}{\text{.5}} = 5{\text{ }}\Omega$
So, we get
$\Rightarrow {I_1} = \dfrac{5}{5}$
$\Rightarrow {I_1} = 1A$
The potential difference between $A$ and $C$ can also be given as
$\Rightarrow {V_{AC}} = {I_1}{R_{AC}}$
Substituting ${I_1}$ and ${R_{AC}}$ from above, we get
$\Rightarrow {V_{AC}} = 1\left( {1.5x} \right)$
$\Rightarrow {V_{AC}} = 1.5x$ … (3)
From (2) and (3)
$\Rightarrow 1.5x = 3$
$\Rightarrow x = \dfrac{3}{{1.5}}$
Finally, $x = 2$
So, the length $AC = 2m$
Hence the correct answer is option (A), $2m$ .

Note
Don’t be confused by the resistance ${r_1}$ , whose value is not given in the question. Don’t try to obtain its value, as it is not possible to find from the information given in the question. The reason for not giving the value of ${r_1}$ is that its value is useless in this question. This is because, as there is no deflection in the galvanometer, the current in the branch containing ${r_1}$ is equal to zero. So, the drop across ${r_1}$ will also be zero. So, the resistance ${r_1}$ has no role in this problem.