Question
Question: In the given network the potential difference between p and q is 2V and \(C_2 = 3C_1\) . Then find t...
In the given network the potential difference between p and q is 2V and C2=3C1 . Then find the potential difference between a and b in V .
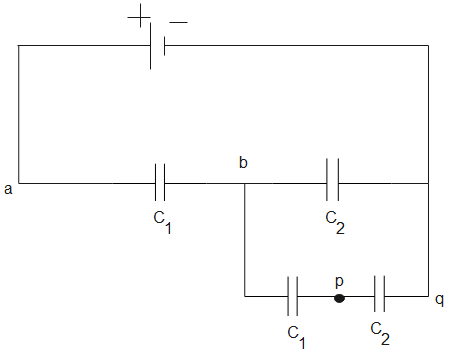
Solution
The figure shows capacitors connected in different combinations between different points. The capacitance is the product of charge and potential of the capacitor. Using this relation and solving the combination of capacitors, we can calculate the potential difference between the given points.
Formulas used:
C=VQ
Complete answer:
Given, the potential difference between p and q is 2V
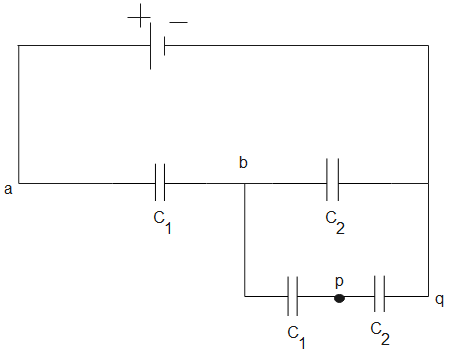
From the figure, we can say that the potential difference between p and q is equal to the potential difference across the capacitor C2
We know that,
C=VQ - (1)
Here, C is the capacitance
Q is the charge on the capacitor
V is the potential difference across the capacitor
For capacitor C2, V2=2V substituting given values in the above equation, we get,
C2=2VQ1⇒Q1=2C2V
Therefore, the charge on the capacitor C2 is 2C2V.
The capacitors between the points b and q are in series, they will be related as-
V2V1=C1C2
Given, C2=3C1, V2=2V. In the above equation, substituting given values to get,
2VV1=C13C1⇒V1=6V
Therefore, the potential drop across the capacitor C1 is 6V.
The total potential across bq is-
V1+V2=6V+2V=8V - (2)
The capacitors between b and q are connected in series, so the equivalent capacitance between b and q is-
C1=C11+C21⇒C1=C11+3C11⇒C1=3C14∴C=43C1
Now capacitors 43C1 and C2 are in parallel.
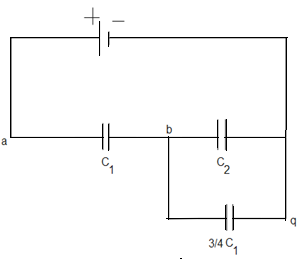
The equivalent capacitance between b and q is-
C′=43C1+C2⇒C′=43C1+3C1⇒C′=415C1
The total charge across bq will be-
Q=415C1(8V)⇒Q=30C1V
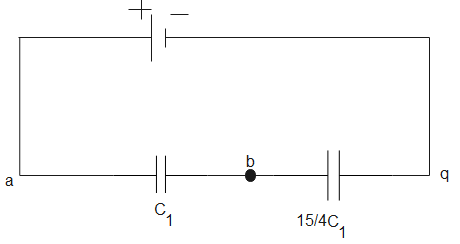
The charge across C1 and 415C1 is the same as they are connected in series and the charge is 30C1V (from eq (2)).
Using eq (1), the potential difference between a and b is-
V=C130C1V⇒V=30V
Therefore, points ab have a potential difference of 30V.
Note:
Capacitors connected in series have the same charge while the capacitors connected in parallel have the same potential. The potential across the wire is the same at all points and changes when an element is connected in between. Two points coincide if they have the same potential.
