Question

In the given network shown in the figure current $1A$ and $2A$ flows across $6\Omega$ and$3\Omega$ resistance, the internal resistance of the battery is

A. $3\Omega$
B. $2\Omega$
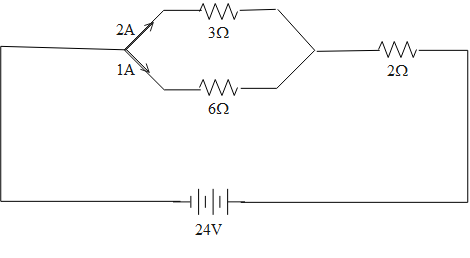
C. $4\Omega$
D. $6\Omega$

Answer 1

The internal resistance of a cell is the obstacle faced by the electrons to flow within the two plates (anode and cathode) inside the cell. The value of the internal resistance of the cell must be very low. In an ideal case for the calculation of a complex circuit, the internal resistance of the object is considered to be zero.
As per the given data,
The current of value$1A$ flows from the resistor of $6\Omega$
The current of value $2A$ flows from a resistor of resistance $3\Omega$ which is parallel to the resistor of $6\Omega$
The voltage across the circuit is $24V$
Formula to be used,
Total current flowing $I={{I}_{1}}+{{I}_{2}}$
The voltage drop across any closed loop $V=I(R+r)$

Complete answer:
The circuit given in the question can be labeled as,

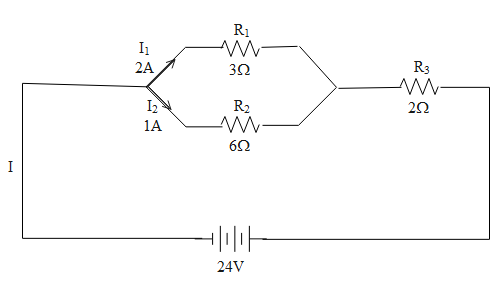
The total current is some of the currents in the two branches parallel to each other
$\begin{aligned} & I={{I}_{1}}+{{I}_{2}} \\\ & \Rightarrow I=2+1 \\\ & \Rightarrow I=3A\ \ldots ...\left( 1 \right) \\\ \end{aligned}$
From the circuit given in the question, the two resistances are connected parallel and these are connected to a resistor $2\Omega$ in series. So the resistance of the circuit will be
$\begin{aligned} & R=\left( \dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{2}}+{{R}_{2}}} \right)+{{R}_{3}} \\\ & \Rightarrow R=\left( \dfrac{6\times 3}{6+3} \right)+2 \\\ & \Rightarrow R=2+2 \\\ & \Rightarrow R=2\Omega \quad \ldots ...\left( 2 \right) \\\ \end{aligned}$
Using Ohm’s law,
$V=I\left( R+r \right)$
Using the given value of voltage and value of current and total resistance of the circuit calculated above. The internal resistance of the cell can be given as,
$\begin{aligned} & 24=3\left( 4+r \right) \\\ & \Rightarrow r=8-4 \\\ & \Rightarrow r=4\Omega \\\ \end{aligned}$

Thus, the correct option showing the true value of the internal resistance used for the circuit mentioned in the question is Option C.

Note:
The internal resistance of a cell can be estimated by using an instrument named potentiometer. It is a kind of external variable resistance to a circuit. We can also control the voltage supplied to a circuit using a potentiometer and compare the internal resistance of two voltage (DC voltage) sources.