Question
Question: In the given network of capacitors, the equivalent capacitance between point \(A\) and \(B\) is 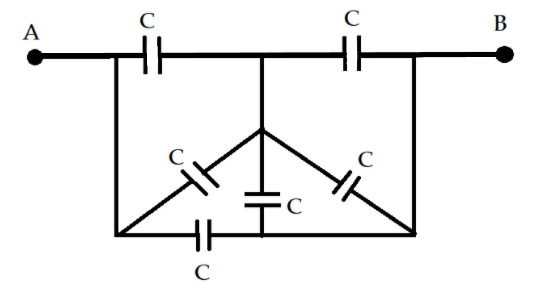
a. 56C
b. 2C
c. 119C
d. 511C
Solution
Here in this question capacitors are connected in different arrangements in a circuit between two given points. A capacitor is generally an electronic device that stores electrical energy in the electric field and it is a passive electronic component as it receives energy.
Formula used:
Parallel connection of the capacitors
CT=CA+CB+....
Series connection of the capacitors
CT=CA+CB+..CA×CB×..
Complete step by step answer:
We will start with the different arrangements of the components and analyze whether which are connected in series connection or parallel connection and then they are calculated separately and then the equivalence capacitor is then evaluated.
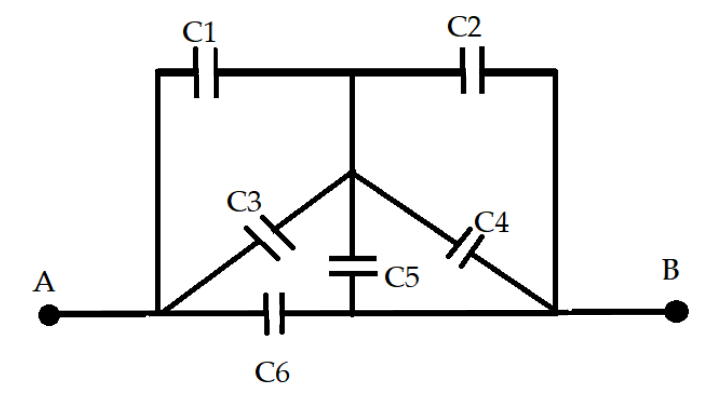
Staring with the rearrangements of the points A and B given on the circuits. All the capacitors have the same capacitance
C1=C2=C3=C4=C5=C6=C
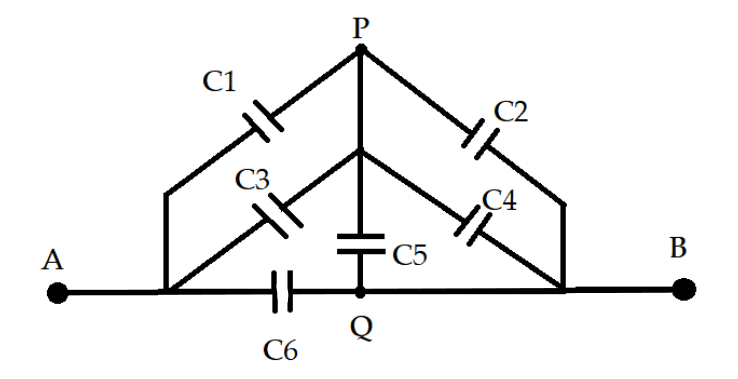
From the figure, it can be concluded that the capacitors C1 and C3 are in the parallel connection between points P , and A hence their equivalent capacitance is given as
CAP=C1+C3
Substitute the values of C1and C3 hence,
CAP=C+C
⇒CAP=2C
Similarly, the between points P and B the capacitors C2,C4 and C5 are in parallel connection hence their equivalent capacitance is given as
CBP=C2+C4+C5
⇒CBP=C+C+C=3C
Now on analyzing, it is found that the capacitor with 3C and 2C are in series hence their equivalent capacitance is given as
C′′′=3C+2C3C×2C
⇒C′′′=56C
Hence the final equivalent capacitance between the points A and B can be given by the parallel connection between C′′′ and C which is given as
CAB=56C+C
⇒CAB=56C+5C=511C
Hence the final equivalent capacitance between the points A and B can be given as 511C.
Hence, the correct answer is option (D).
Note: Here it is noted that the equivalence formula of capacitors is different from the other electronic components like resistance. Hence one should not get confused between the equivalence formula between resistance and capacitors. For resistance connected in series, the equivalence formula is given by R=R1+R2+... , and for resistance connected in parallel, the formula is given as R=R1+R2+..R1R2....
