Question

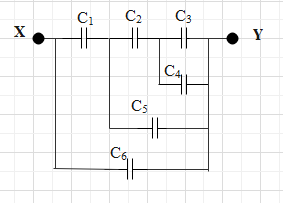
In the given network of capacitors as shown in figure, given that ${{C}_{1}}={{C}_{2}}={{C}_{3}}=400pF$ and ${{C}_{4}}={{C}_{5}}={{C}_{6}}=200pF$ . The effective capacitance of the circuit between X and Y is:

A. 800pF
B. 205pF
C. 600pF
D. 410pF

Answer 1

Find the mathematical expression for the total capacitance of a circuit with capacitors connected in parallel and capacitors connected in series. First simplify the given circuit to find out if the capacitors are connected in series or parallel. Then solve the circuit accordingly.

Complete answer:
A capacitor is an electronic device which stores electrical energy inside an electric field. The capacitor stores energy in the form of electrical charge which produces a potential difference between the two plates of the capacitor. It is a passive electrical component.
If two capacitors ${{C}_{1}}$ and ${{C}_{2}}$ are connected in series to each other the total capacitance of the system is given as,
$\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}$
If two capacitors ${{C}_{1}}$ and ${{C}_{2}}$ are connected in parallel to each other the total capacitance of the system is given as,
$C={{C}_{1}}+{{C}_{2}}$
Now, simplifying the given circuit in the question, the capacitance ${{C}_{3}}$ and ${{C}_{4}}$ are in parallel connection.
The equivalent capacitance is ${{C}_{eq}}={{C}_{3}}+{{C}_{4}}=400pF+200pF=600pF$
This equivalent capacitance is in series with capacitor ${{C}_{2}}$ .
The equivalent capacitance is,
$\begin{aligned} & \dfrac{1}{C}=\dfrac{1}{{{C}_{2}}}+\dfrac{1}{{{C}_{eq}}}=\dfrac{1}{400}+\dfrac{1}{600} \\\ & \dfrac{1}{C}=\dfrac{5}{1200} \\\ & C=240pF \\\ \end{aligned}$
This equivalent capacitance is in parallel with the capacitor ${{C}_{5}}$ .
The equivalent capacitance will be,
${{C}_{eq}}=C+{{C}_{5}}=240pF+200pF=450pF$
This equivalent capacitance is again in series connection with capacitor ${{C}_{1}}$
The equivalent capacitance is,
$\begin{aligned} & \dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{eq}}}=\dfrac{1}{400}+\dfrac{1}{450} \\\ & \dfrac{1}{C}=\dfrac{17}{3600} \\\ & C=211.76pF \\\ \end{aligned}$
This equivalent capacitance is in parallel with ${{C}_{6}}$ .
The equivalent capacitance will be,
$\begin{aligned} & {{C}_{eq}}=C+{{C}_{6}} \\\ & {{C}_{eq}}=211.76+200 \\\ & {{C}_{eq}}=411.76pF \\\ \end{aligned}$
So, we can say that the equivalent capacitance is almost 410pF.

So, the correct answer is “Option D”.

Note:
Capacitance of a capacitor can be defined as the ability of the capacitor to store energy in the form of the electrical charge. It is the ratio of the change in electric charge to the corresponding change in electric potential of the capacitor. The SI unit of the capacitance is Farad.