Question

In the given figures sides $AB$ and $BC$ and median $AD$ of a $\Delta ABC$ are respectively proportional to sides $PQ,QR$ and median $PM$ of $\Delta PQR$ . show that triangle $\Delta ABC \sim \Delta PQR$.

Answer 1

Hint: In order to solve this question, we have to apply similarity rules of triangles and in which side and angles helps us to show the similarities of these triangles.

Complete step-by-step answer:

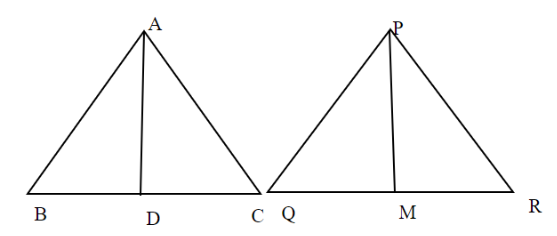
According to given question,
$\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{AD}}{{PM}} - - - - - \left( 1 \right)$
In $\Delta ABC$, since $AD$ is the median,
$BD = CD = \dfrac{1}{2}BC$
Or $BC = 2BD - - - - - \left( 2 \right)$
Similarly, $PM$ is the median,
$QM = RM = \dfrac{1}{2}QR$
Or $QR = 2QM - - - - - \left( 3 \right)$
Substituting the value of $BC,QR$ in equation (1), we get
$\dfrac{{AB}}{{PQ}} = \dfrac{{2BD}}{{2QM}} = \dfrac{{AD}}{{PM}}$
$\dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QM}} = \dfrac{{AD}}{{PM}} - - - - - \left( 4 \right)$
Since all three sides are proportional.
Therefore, by SSS similarity rule,
$\Delta ABD \sim \Delta PQM$
Hence,$\angle B = \angle Q - - - - - - \left( 5 \right)$,
corresponding angles of similar triangles are equal.
In $\Delta ABC\& \Delta PQR$
Using (5), we get
$\angle B = \angle Q$
Given, $\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}}$
Hence by SAS Similarity of triangle.
$\Delta ABC \sim \Delta PQR$

Note: Whenever we face these types of questions the key concept is that we have to take small triangles and by similarity rules show them similar by which we get two sides or one sides and one angle equality and we will easily get our desired answer.