Question
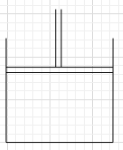
Question: In the given figure, walls of the container and the piston are weakly conducting. The initial pressu...
In the given figure, walls of the container and the piston are weakly conducting. The initial pressure, volume and temperature of the gas are 200kPa, 800cm3 and 100K respectively. Find the pressure and the temperature of the gas if it is (a) slowly compressed (b) suddenly compressed to 200cm3 (γ=1.5)
Solution
When the gas is compressed slowly, the gas maintains its equilibrium state. This means that the temperature of the gas remains constant. Use the gas equation to find the final pressure and temperature. When the gas is suddenly compressed, it undergoes adiabatic process. In a adiabatic process, PVγ=constant and
TVγ−1=constant
Formula used:
PV=nRT
PVγ=constant
TVγ−1=constant
where P, V, n and T are the pressure, volume , number of molecules and temperature of the gas and R is the gas constant.
Complete step by step answer:
When the gas is compressed slowly, the gas maintains its equilibrium state. This means that the temperature of the gas remains constant. It is given that the initial temperature of the gas is 100K. Therefore, when the gas is slowly compressed to a volume of 200cm3, its temperature remains 100K.To find the final pressure of the gas we shall use the gas equation PV=nRT, where P, V, n and T are the pressure, volume , number of mole and temperature of the gas. R is the gas constant.For a given gas n is constant. Therefore, if T is constant then PV is also constant. This means that the product of initial pressure and volume is equal to the product of final pressure and volume.
i.e.PiVi=PfVf.
Here, Pi=200kPa, Vi=800cm3 and Vf=200cm3.
Then,
⇒(200kPa)(800cm3)=Pf(200cm3)
∴Pf=(200cm3)(200kPa)(800cm3)=800kPa.
This means that when the gas is compressed to 200cm3 slowly, its pressure increases to 800kPa.
(b) When the gas is suddenly compressed, it undergoes adiabatic process.
In an adiabatic process, PVγ=constant …. (i).
This means that PiViγ=PfVfγ.
Substitute the known values.
(200kPa)(800cm3)1.5=Pf(200cm3)1.5
⇒Pf=(200cm3)1.5(200kPa)(800cm3)1.5
⇒Pf=(200cm3)1.5(200kPa)(800cm3)1.5 ⇒Pf=1600kPa.
In adiabatic processes, the temperature and volume are related as,
TVγ−1=constant.
This means that TiViγ−1=TfVfγ−1.
Substitute the known values.
⇒(100K)(800cm3)1.5−1=Tf(200cm3)1.5−1
⇒Tf=(200cm3)0.5(100K)(800cm3)0.5 ∴Tf=200K.
Therefore, when the gas is suddenly compressed to a volume of 200cm3, its temperature increases to 200K and its pressure also increases to 1600kPa.
Note: Adiabatic process is a thermodynamic process in which there is no transfer of heat in or out of the gas. This means that neither the has absorbs heat nor it gives out heat.If you do not know the relation be temperature and volume, then you can use the gas equation to find the final temperature.
