Question

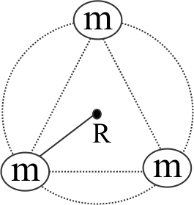
In the given figure, there is a hypothetical planet of mass $M$ at the centre and three moons each of mass $m$ revolves around the planet in the same orbit. The triangle formed in the configuration is an equilateral triangle. If the orbital speed of each moon such that they maintain this configuration is given by $n\sqrt {\dfrac{G}{R}\left( {\dfrac{m}{{\sqrt 3 }} + M} \right)}$ then find $n$. (Neglect the radius of the planet and the moons)

Answer 1

Consider a single moon and find the gravitational forces on that moon due to the planet and the other moons towards the centre of the planet. The sum of these forces towards the centre will be equal to the centripetal force due to which the moons are revolving around the planet.
The gravitational force between two masses ${m_1}$ and ${m_2}$ separated by a distance $r$ is given by ${F_g} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$ where $G$ is the gravitational constant.
The centripetal force due to which a body of $m$ revolving in an orbit of radius $r$ with orbital velocity $v$ is given by ${F_c} = \dfrac{{m{v^2}}}{r}$ .

Complete step by step answer:
Let us first consider a moon. The gravitational forces acting on this moon will be due the other two moons and the planet.
We know that the gravitational force between two masses ${m_1}$ and ${m_2}$ separated by a distance $r$ is given by ${F_g} = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$ where $G$ is the gravitational constant.
As the triangle formed in the configuration is an equilateral triangle so the distance between any two moons will be $\sqrt 3 R$ .
So, the gravitational force due to a moon,
${F_{mm}} = \dfrac{{G{m^2}}}{{{{\left( {\sqrt 3 R} \right)}^2}}} = \dfrac{{G{m^2}}}{{3{R^2}}}$
Now, the gravitational force due to the planet,
${F_{mM}} = \dfrac{{GMm}}{{{R^2}}}$
The total force on the moon towards the centre of the planet
$F = {F_{mM}} + 2{F_{mm}}\cos 30^\circ$
This total force towards the centre will be equal to the centripetal force due to which the moons are revolving around the planet.
We know that the centripetal force due to which a body of $m$ revolving in an orbit of radius $r$ with orbital velocity $v$ is given by ${F_c} = \dfrac{{m{v^2}}}{r}$ .
Therefore substituting the values we have
$\dfrac{{m{v^2}}}{R} = \dfrac{{GMm}}{{{R^2}}} + 2 \times \dfrac{{G{m^2}}}{{3R}} \times \dfrac{{\sqrt 3 }}{2}$
On further solving we have
${v^2} = \dfrac{{GM}}{R} + \dfrac{{Gm}}{{\sqrt 3 R}}$
On simplifying we have
$v = \sqrt {\dfrac{G}{R}\left( {\dfrac{m}{{\sqrt 3 }} + M} \right)}$
On comparing our result from that given in the equation we have
$n = 1$ which is the final answer.

Note: A centripetal force is that force which is necessary to keep a body moving a curved path. The direction of this force is always perpendicular to the motion of the body and towards the centre of rotation which is a fixed point and also called centre of curvature.