Question
Question: In the given figure the wedge is fixed, the pulley is frictionless and the string is light. Surface ...
In the given figure the wedge is fixed, the pulley is frictionless and the string is light. Surface AB is frictionless whereas AC is rough, if the block of mass 3m slides down with constant velocity, then the coefficient of friction between surface AC and the block is
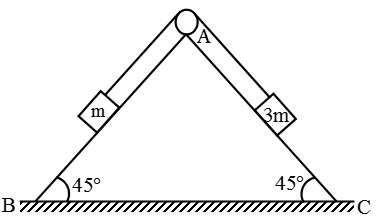
(A) 31
(B) 32
(C) 21
(D) 34
Solution
Hint
We use Newton’s second law of motion as well as the formula for friction force to solve this question. A free body diagram should be made first to understand all the forces acting on both the blocks. We find the total tension force acting on the left side and right side of the wedge and then equate them to find the value of the coefficient of friction.
Friction force, f=μFN
Here, the friction force is represented by f, The coefficient of friction is represented by μ, and The normal force is represented by FN
Complete step by step answer
The system is under the influence of gravity, so we take the acceleration of both the blocks as acceleration due to gravity, that is, a=g
Free body diagram of the system,
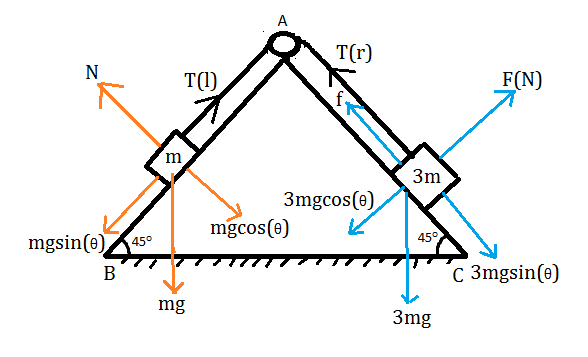
θ=45∘
From the free body diagram, the total tension force on the left side of the wedge
⇒Tl=mgsin(45∘)
From the free body diagram of the right block, FN=3mgcos(45∘)
The friction force is the product of normal force and coefficient of friction.
Friction force is f=μFN
⇒f=μ×3mg×cos(45∘)
On the right side of the wedge, the tension force is the difference between friction force and force due to gravity.
The total force acting on the right block is,
⇒Tr=3mgsin(θ)−f
⇒Tr=3mgsin(45∘)−μ×3mgcos(45∘)
Since the same string is attached to both the blocks, we take forces on both the tension forces as equal,
⇒Tr=Tl
⇒3mgsin(45∘)−μ×3mg×cos(45∘)=mgsin(45∘)
⇒μ×3mg×cos(45∘)=2mgsin(45∘)
⇒3μ=2tan(45∘)
⇒3μ=2
⇒μ=32
The coefficient of friction is 32.
Hence option (B) 32 is the correct answer.
Note
The angle 45∘ is the angle between the direction of weight and the horizontal component of it, which is nothing but the angle of inclination. We take cos(θ) and sin(θ) under consideration in an inclined plane because the force acting on a body in an inclined plane is divided into horizontal and vertical components. The magnitude of the forces depends on the angle at which the force is acting on it.
