Question
Question: In the given figure the wedge is fixed, pulley is light and frictionless and string is light Surface...
In the given figure the wedge is fixed, pulley is light and frictionless and string is light Surface AB is frictionless whereas AC is rough If the block of mass 3m slides down with constant velocity, then the coefficient of friction between surface AC and the block is
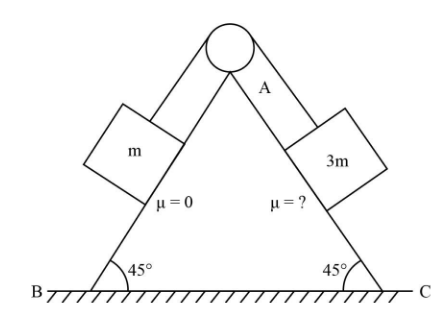
A. 31
B. 32
C. 21
D. 34
Solution
This question is based on the concept of mass and pulley. There are two blocks available connected by the pulley. One block of mass 3mslides down and tension is acting on the string connecting the two blocks. On another block that has mass m moving with constant velocity and tension T is acting on the string and also mgsinθ acting on the block. We have to equate the equations and find the coefficient of friction.
Complete step by step answer:
We know that if the block is moving with constant velocity then the acceleration becomes zero. First, we consider the mass m. On this block of m, there are several forces act on the block, one is tension force and another force is mgsinθ.
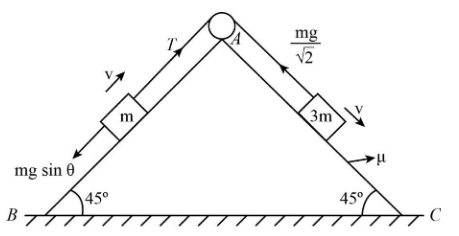
Now, we can equate the two forces we get,
T=mgsinθ
Here, θ is 45∘.
Substitute the values in the above equation we get,
T=mgsin45∘ ⇒T=2mg
Now, on the second block, the tension is the same. So, we can calculate the coefficient of friction of block 3m.
Now , the expression of coefficient of friction is given as,
f=μN
Here, μ is the coefficient of friction and N is the normal force.
Substitute the values in the above equation we get,
Therefore, the coefficient of friction is 32.
Thus, the correct option is B.
Note: In this question, the students must know how to resolve forces and must have knowledge of the term frictional force and tension force. On the block of mass 3m the frictional force is 3mgsin45∘ because two components are formed one is normal 3mgcos45∘ and another is frictional force 3mgsin45∘. And the tension force also acts on the string. Since the pulley is frictionless, the tension remains the same on both sides.
