Question

In the given figure the value of $\cos ecA$ is

Answer 1

Hint : The given figure is a right angle triangle. In the right angle triangle three sides are hypotenuse, opposite and adjacent and all the trigonometry ratios are applicable for the right angle triangle. In the given figure the value of perpendicular and base are given so we first find the hypotenuse by using Pythagoras theorem. Then we get the required value of $\cos ecA$ by using the formula of $\cos ecA$ .

Complete step-by-step answer :
Given figure

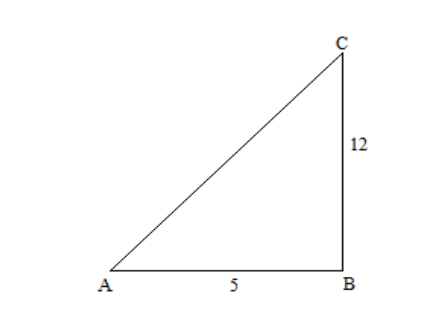
From figure
Perpendicular (BC) $= 12$
Base (AB) $= 5$
The value of Hypotenuse (AC) is not given in the figure so we first find the hypotenuse by using Pythagoras theorem
We know that by Pythagoras theorem
${\left( {hypotenuse} \right)^2} = {\left( {opposie} \right)^2} + {\left( {Adjacent} \right)^2}$
${\left( {AC} \right)^2} = {\left( {BC} \right)^2} + {\left( {AB} \right)^2}$
On putting the value of BC and AB from figure
${\left( {AC} \right)^2} = {\left( {12} \right)^2} + {\left( 5 \right)^2}$ ----------- $\left( 1 \right)$
Since ${(12)^2} = 144$ and ${\left( 5 \right)^2} = 25$
On putting this value in the equation $\left( 1 \right)$
$\Rightarrow {\left( {AC} \right)^2} = 144 + 25 \\\ \Rightarrow {\left( {AC} \right)^2} = 169 \;$
On taking square root on both side
$\Rightarrow AC = \sqrt {169}$
Since $\sqrt {169} = 13$
Therefore $AC = 13$
Hence hypotenuse is 13.
Now, we have to calculating the value of $\cos ecA$
Formula for $\cos ecA$
$\cos ecA = \dfrac{{hypotenuse}}{{Opposite}}$
$\cos ecA = \dfrac{{AC}}{{BC}}$
Since the value of $AC = 13$ and $BC = 12$
On putting this values in above expression
$\cos ecA = \dfrac{{13}}{{12}}$
Hence, the required value of $\cos ecA$ is $\dfrac{{13}}{{12}}$ .
So, the correct answer is “ $\dfrac{{13}}{{12}}$”.

Note : For this type of problem we must know the property of right angle triangle and also by using the relation between its side we get the formula of all trigonometric ratios like sine, cosine, tangent, cosecant, secant, and cotangent, i.e. they can be written as sin, cos, tan, cosec, sec, and cot. Here we also use Pythagoras theorem which also gives important relation between sides of the right angle triangle.