Question

In the given figure the steady state current I is:

$\left( A \right)zero$
$\left( B \right)0.6A$
$\left( C \right)0.9A$
$\left( D \right)1.5A$

Answer 1

In steady state the capacitor acts as an open circuit no current flows through it. Now we will calculate the net equivalent resistance of the circuit. Voltage is given with the help of ohm’s law formula to calculate the current flowing in the circuit. In this way we can find the value of I.

Complete step by step solution:

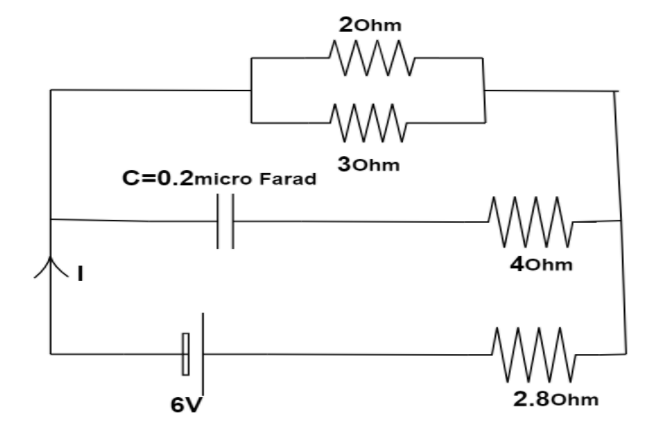
We need to calculate the steady state current.And we know that in steady state there is no current in the capacitor branch as in steady state the capacitor has a voltage across it, but no current flows through it hence it acts as an open circuit in steady state.
Now the diagram will look like,

As the capacitor does allow any current to pass through it then the resistor present in that branch also allows zero current.
Now the equivalent circuit will look like after removing 4ohm resistor,

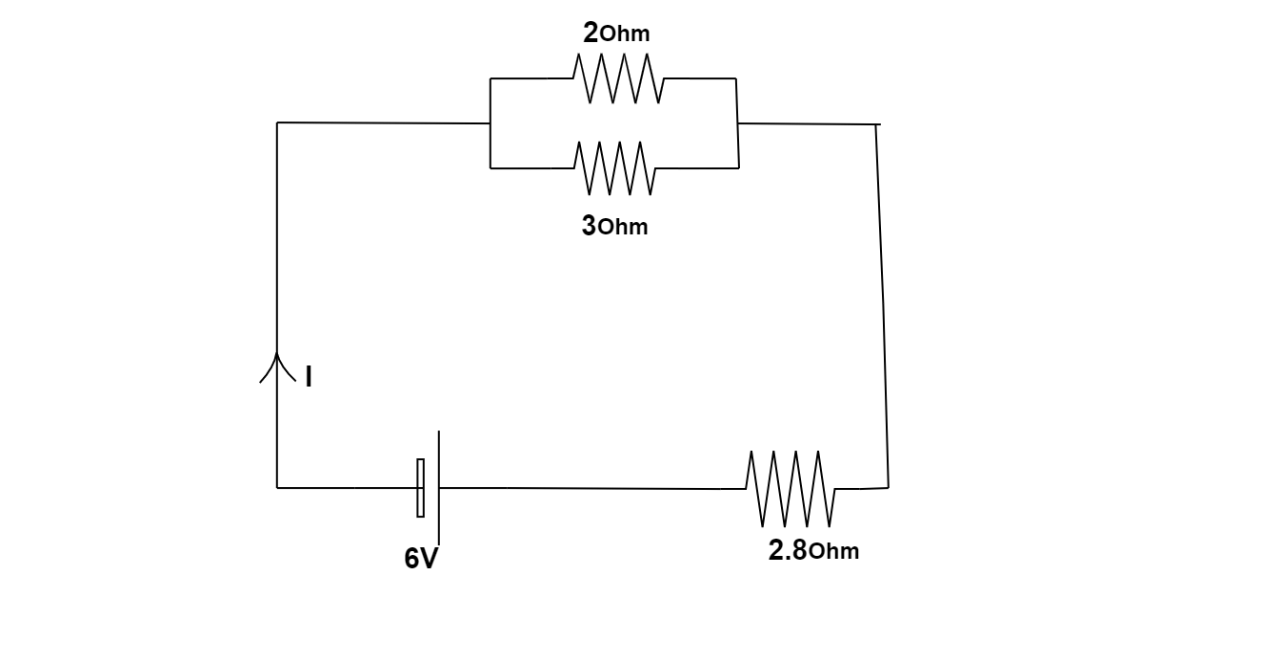
Now calculating the net equivalent resistance we will get,
Resistor 2ohm and 3ohm are connected parallel to each other hence the equivalent resistance in that branch will be,
Let $R23$ be the equivalent resistance of 2ohm and 3ohm and $R2$,$R3$ are respective resistance
$R23 = R2||R3$
$\Rightarrow R23 = \dfrac{{R2 \times R3}}{{R2 + R3}}$
Putting the respective value we will get,
$R23 = \dfrac{{2 \times 3}}{{2 + 3}}\Omega$
$\Rightarrow R23 = \dfrac{6}{5}\Omega$
Now $R23$ is in series with 2.8ohm.
Hence $\operatorname{Re} q$ = equivalent resistance will be,
$\operatorname{Re} q = R23 + 2.8\Omega$
Putting the value of $R23$ in the above equation we will gte,
$\operatorname{Re} q = \dfrac{6}{5}\Omega + 2.8\Omega$
Further simplifying we will get,
$\operatorname{Re} q = 1.2\Omega + 2.8\Omega$
$\Rightarrow \operatorname{Re} q = 4\Omega$
Now from the ohm’s law we know,
$V = IR$
Where,
V = Voltage
I = Current
R = Resistance
In place of R we will write $\operatorname{Re} q$ as we find net steady state current.
Now we can write,
$V = IR{\text{eq}}$
Rearranging the above equation we will get,
$I = \dfrac{V}{{R{\text{eq}}}}$
We know from the diagram,
$V = 6V$
And we calculated the value
$R{\text{eq = 4}}\Omega$
Putting the respective value we can get the current,
$I = \dfrac{{6V}}{{4\Omega }}$
$\Rightarrow I = 1.5A$
Therefore the current option is $\left( D \right)$.

Note:
Always keep in mind whenever you are calculating some problem under steady state conditions, then always keep the capacitor as an open circuit and the inductor as a short circuit. In steady state the voltage across the inductor is zero while in case of capacitor the current across is infinity.