Question

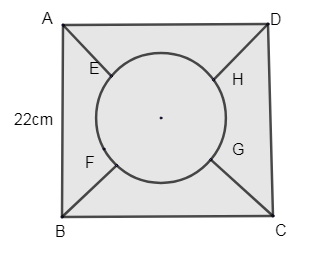
In the given figure, the square ABCD is divided into five equal; parts, all having the same area. The central part is circular and the lines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22cm. Find the perimeter of the part ABEF.

Answer 1

Hint: Find the area of the given and find the area of the circle which is ${{\dfrac{1}{5}}^{th}}$of the total area. Take O as the central point. Find the value of OA, AE and find the value of arc EF. Add all the values to get the perimeter of part ABEF.

Complete step-by-step Solution:
Given a square ABCD, we know that in a square all sides are equal and all the angles are ${{90}^{\circ }}$.
Given that AB = 22cm, where AB is the side of a square.
We are told that all sides are equal.
So, AB = BC = CD = DA = 22cm.
Area of the square is given as the square of the side.
i.e. Area of square $={{\left( side \right)}^{2}}$.
Here, the sides of the square are AB, BC, CD and DA which is equal to 22cm.
$\therefore$Side of square = 22cm
$\therefore$Area of square $={{\left( 22 \right)}^{2}}=22\times 22=484c{{m}^{2}}$

It is said that the square ABCD is divided into 5 equal parts in terms of area.
We know the total area of the square as $484c{{m}^{2}}$. Out of these 5 equal parts, one part is the circle inscribed inside the square. To find the area of the circle we need to divide the total area by 5.
$\therefore$Area of circle$=\dfrac{1}{5}\times$area of square
$=\dfrac{1}{5}\times 484=96.8c{{m}^{2}}$
Area of the circle is given by the formula, $\pi {{r}^{2}}$. We need to find the radius, r of the circle.

& \therefore \pi {{r}^{2}}=96.8 \\\ & \Rightarrow {{r}^{2}}=\dfrac{96.8}{\pi }=30.81 \\\ & \therefore r=\sqrt{30.81}=5.55cm \\\ \end{aligned}$$ $$\therefore $$Radius of the central part = 5.55cm. Let us consider O as the center of the circle thus O also becomes the center of the square. We know the diagonal of a square is given by $$\sqrt{2}a$$, where ‘a’ is the side of the square. Let the diagonal of square AC = $$\sqrt{2}a$$. $$\begin{aligned} & AC=OA+OC \\\ & \therefore OA=OC=\dfrac{AC}{2} \\\ \end{aligned}$$ i.e. Diagonals of the square are equal in length and bisect each other. $$\therefore OA=\dfrac{\sqrt{2}a}{2}=\dfrac{\sqrt{2}\times 22}{2}=11\sqrt{2}cm$$ From the figure we can say that length of AE is equal to length of BF. $$AE=OA-OE$$[from the figure] $$\therefore AE=BF=OA-OE$$ OE is equal to the radius of the circle = 5.55cm. $$\begin{aligned} & \therefore AE=BF=11\sqrt{2}-5.55\left[ \because \sqrt{2}=1.414 \right] \\\ & AE=\left( 11\times 1.414 \right)-5.55 \\\ & AE=BF=9.96cm \\\ \end{aligned}$$ The arc of circle EF$$=\dfrac{1}{4}\times $$circumference of the circle We know the circumference of the circle $$=2\pi r$$. $$\therefore arcEF=\dfrac{1}{4}\times 2\pi r=\dfrac{1}{4}\times 2\pi \times 5.55=8.72cm$$ Hence, perimeter of point ABEF = AB + AE + EF + BF = 22 + 9.96 + 8.72 + 9.96 = 50.64cm $$\therefore $$Perimeter of part ABEF = 50.64cm. Note: Since it is a square, the area of part ABEF is equal to the area of part BFGC, CGHD and DHEF. And their areas are the same as mentioned in the question. The area of the circle is$$96.8c{{m}^{2}}$$, which was one part of the circle. Similarly, the area of ABEF, BFGC, CGHD and DHEF is equal to $$96.8c{{m}^{2}}$$. By adding all this we get the total area as $$484c{{m}^{2}}$$.