Question

In the given figure, the pulley is massless and frictionless. There is no friction between the body and the floor. The acceleration produced in the body when it is displaced through a certain distance with force $P$ will be:

A) $\dfrac{P}{M}$
B) $\dfrac{P}{{2M}}$
C) $\dfrac{P}{{3M}}$
D) $\dfrac{P}{{4M}}$

Answer 1

Hint
Here, firstly in the string so tension $T$ will be applied and it will balance by the applied force $P$. And then use Newton's second law of motion.

Complete step-by-step answer:
As it is given that pulley is massless and frictionless and force $P$ is applied on it so there occurs tension in the string. As shown below

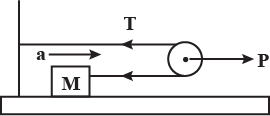
As, there are two strings the same tension $T$ is applied on the two strings. As, total tension is balanced by the force $P$ before the motion of the mass therefore,
⇒ $2T = P$
⇒ $T = \dfrac{P}{2}$………………….. (1)
Where, $T$ is tension in the strings
$P$ is the force applied on the pulley.
Now, when we apply the force $P$ then there will be the acceleration of the body through some distance then we can apply Newton's second law of motion. Which states that force applied on the body is equal to the product of mass and acceleration of the body.
⇒ $P = Ma$
Where, $M$ is the mass of the body
$a$ is the acceleration of the body
Now this force is only equal to the tension in the one string which is attached to the wall therefore,
⇒$Ma = T$
⇒ $a = \dfrac{T}{M}$………………… (2)
Now, put the value of T from equation (1) into the equation (2), we get
⇒ $a = \dfrac{P}{{2M}}$

Note:
Firstly here when the force $P$ is applied it will balance the tensions in the strings which are acting in the opposite directions to that of force $P$. Now when the force increases such that this force is greater than the total tension in the strings then the body of mass $m$ will accelerate now only the opposite force acting is the tension $T$ in the string which is attached with the wall.