Question
Question: \- In the given figure, the position-time graph of a particle of mass 0.1 kg is shown. The impulse a...
- In the given figure, the position-time graph of a particle of mass 0.1 kg is shown. The impulse at t=2sec is:
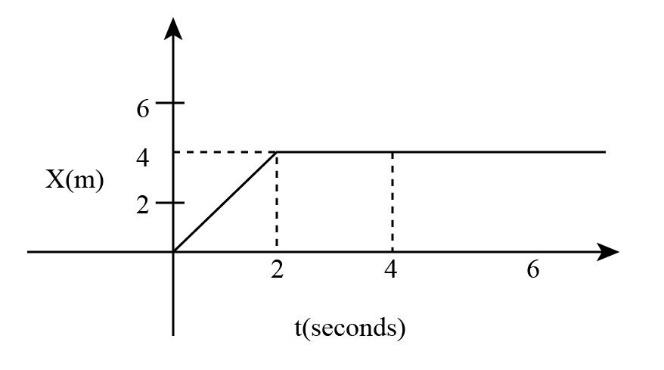
(A) 0.2kgmsec−1
(B) −0.2kgmsec−1
(C) 0.1kgmsec−1
(D) −0.4kgmsec−1
Solution
You need to apply the concept of calculation of velocity and the impulse. You first need to calculate the final and initial velocity of the particle with the help of the graph. Then you need to calculate the impulse by using the formula, which is the impulse is equal to change in momentum.
Complete step by step answer: Given:
The mass of the particle is m=0.1kg.
As we know, the expression for the velocity of an object is given as,
v=dtdx ⟹v=tf−tidf−di
Here, df is the final position of the particle at instant of time interval tf, and di is the initial position of the particle at instant of time interval ti.
Now we substitute the values in the above expression, to get the initial velocity between t=0 and t=2s,
vi=2s−0s4m−0m ⟹vi=2s4m ⟹vi=2msec−1
Further, the final velocity of the particle at t=2sec will be zero, that is vf=0.
We know the expression for the impulse can be given as,
I=Δv ⟹I′(vf−vi)
Here, m is the mass of the particle, vf is the final velocity of the particle, and vi is the initial velocity of the particle.
Again we substitute the values in the above expression, to get the impulse of the particle at t=2sec.
I=0.1kg×(0−2msec−1) ⟹I=−0.2kgmsec−1
Therefore, the impulse of the particle at the time interval t=2sec is −0.2kgmsec−1.
Thus, option (B) is correct.
Note:
You can make a mistake by calculating the impulse of the particle as positive. The impulse of the particle in this question will be negative, as the final velocity of the particle is zero. Also remember that the mass of the particle is the same.
