Question

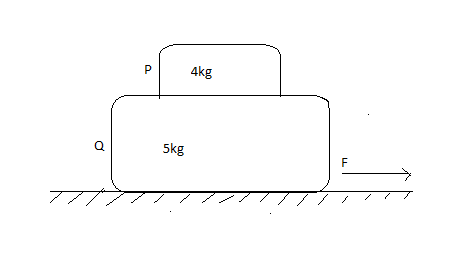
In the given figure, the coefficient of friction between ${\text{4Kg}}$and ${\text{5Kg}}$ blocks is $0.2$ and between ${\text{5Kg}}$ block and ground is $0.1$ respectively. Choose the correct statements.
a. Minimum force needed to cause the system to move is ${\text{17N}}$.
b. When force is ${\text{4N}}$ static friction at all surfaces is 4N to keep the system at rest.
c. Maximum acceleration of ${\text{4Kg}}$ block is $2m{s^{ - 2}}$
d. Slipping between ${\text{4Kg}}$ and ${\text{5Kg}}$ blocks start when $F$ is $> 17N$.

Answer 1

Force accelerates the body at rest and it tends the object to come at rest when it accelerates. Hence the force is the product of mass and acceleration. The net force is the total amount of forces acting on a body. Many forces acting on a body if it is in motion or at rest. When the body is in motion, the frictional force is one of the forces acting on a body. This frictional force is the resistive force acting on a body in motion. It makes the body come to rest.

Complete step by step answer:
From the diagram, there are two blocks of ${\text{4Kg}}$ and ${\text{5Kg}}$. $0.2$ is the friction of coefficient between two surfaces. And the coefficient of friction in between the blocks and the ground is $0.1$.

The force to move the system can be found by the formula $\mu Mg$. Applying the values in the formula, therefore
$\Rightarrow \mu Mg = 0.1(4 + 5)10$
On some simplification we get,
$\therefore \mu Mg = 9N$

From this value, the force needed to move the system is ${\text{9N}}$. But in option A the minimum force needed to move the system is ${\text{17N}}$. Hence the option A is incorrect.

The system is already moving with the force. Hence the option B is incorrect.

The acceleration for the block $4Kg$can be found by$\mu g$. Therefore the value for the acceleration is 0.2 \times 10m{s^{ - 2}}$$$$ \Rightarrow 2m{s^{ - 2}}. The option C also suggests the value we found. Hence the option C is correct.

Slipping between the block occurs when the block of $4Kg$ attains the maximum acceleration. The maximum acceleration of the block of $4Kg$ is $2m{s^{ - 2}}$. The force when the block attains maximum acceleration causes the block to slip is,
$F = ma + {F_r}$
$\Rightarrow F = ma + \mu Mg$
Substitute the values we get,
$\Rightarrow F = 2(9) + 0.1(9)(10)$
On multiply the bracket terms we get
$\Rightarrow F = 18 + 9$
Let us add the terms we get,
$\therefore F = 27N$
The slipping between two blocks starts when the force is greater than $27N$. Therefore the D is incorrect.

Hence, we can conclude that the correct answer is option (C).

Note: The force which is the result of the motion is equal to the product of mass and acceleration ma. The force which is acting on a body is equal to the product of the mass and the acceleration due to gravity $\;mg$.
The coefficient of friction $\mu$is the ratio of forces resisting the body to move. The rough surface is the cause of this frictional force.