Question
Question: In the given figure, TBP and TCQ are tangents to the circle whose center is O. Also, \(\angle PBA = ...
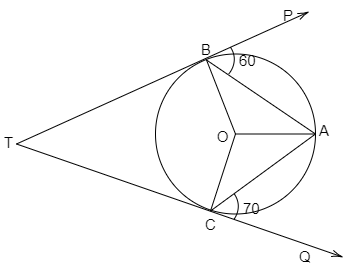
In the given figure, TBP and TCQ are tangents to the circle whose center is O. Also, ∠PBA=60∘ and ∠ACQ=70∘. Determine ∠BAC and ∠BTC.
A. 50∘,60∘
B. 60∘,70∘
C. 50∘,70∘
D. 50∘,80∘
Solution
Use the concept of radius making the right angle at the point of contact with the tangent to find the angle and using the property of isosceles triangle formed by radii of the circle to find the angle contributing to ∠BAC. After that use of the property, the angle subtended by an arc at the center of a circle is double that of the angle that the arc subtends at any other given point on the circle. After that use the property of the sum of opposite angles in a quadrilateral we find the value of ∠BTC.
Complete step by step answer:
We are given the measure of an angle ∠PBA=60∘ and ∠ACQ=70∘.
Use the property of tangents that the radius makes a right angle with the tangent at the point of contact.
⇒∠OBP=90∘
We can write,
∠OBP=∠OBA+∠ABP
Substitute the values,
⇒90∘=∠OBA+60∘
Bring all constant values to one side of the equation,
⇒∠OBA=90∘−60∘
Subtract the values,
⇒∠OBA=30∘
Now we know that OA=OB as they both are radii of the same circle.
So, triangle OAB is an isosceles triangle.
From the property of the isosceles triangle, the angles opposite to equal sides are equal.
⇒∠OAB=∠OBA
Substitute the values,
⇒∠OAB=30∘ ….. (1)
Also, at point C,
⇒∠OCQ=90∘
We can write,
∠OCQ=∠OCA+∠ACQ
Substitute the values,
⇒90∘=∠OCA+70∘
Bring all constant values to one side of the equation,
⇒∠OCA=90∘−60∘
Subtract the values,
⇒∠OCA=20∘
Now we know that OA=OC as they both are radii of the same circle.
So, triangle OAC is an isosceles triangle.
From the property of the isosceles triangle, the angles opposite to equal sides are equal.
⇒∠OAC=∠OCA
Substitute the values,
⇒∠OAC=20∘ ….. (2)
We know that,
⇒∠BAC=∠OAB+∠OAC
Substitute the values from equation (1) and (2),
⇒∠BAC=30∘+20∘
Add the terms,
⇒∠BAC=50∘
From the property of the circle, the angle subtended by an arc at the center of a circle is double that of the angle that the arc subtends at any other given point on the circle.
⇒∠BOC=2∠BAC
Substitute the value of ∠BAC,
⇒∠BOC=2×50∘
Multiply the terms,
⇒∠BOC=100∘
Now we have a quadrilateral OBTC. Then the sum of opposite angles is 180∘.
We have opposite angles ∠BTC and ∠BOC.
⇒∠BTC+∠BOC=180∘
Substitute the value of ∠BOC,
⇒∠BTC+100∘=180∘
Bring all constant values to one side of the equation,
⇒∠BTC=180∘−100∘
Subtract the values,
⇒∠BTC=80∘
Thus, ∠BAC=50∘ and ∠BTC=80∘
Hence, option (D) is the correct answer.
Additional Information: The radius of the circle is perpendicular to the tangent at the point of contact.
An isosceles triangle has two sides of equal length and the angles opposite to equal sides are equal in measure.
The angle subtended by an arc at the center of a circle is double that of the angle that the arc subtends at any other given point on the circle.
In any quadrilateral, the sum of opposite sides is equal to 180∘.
Note: Students many times get confused with angles given in the diagram i.e. ∠PBA=60∘ and ∠ACQ=70∘ as the angles made by radius with the tangents. Keep in mind radius is always perpendicular to the tangent at the point of contact. Always change the sign from negative to positive and vice versa when shifting the values from one side to another.
