Question

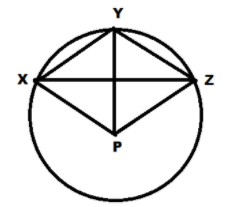
In the given figure, P is the Centre of the circle. Prove that:

$\angle XPZ = 2(\angle XZY + \angle YXZ)$

 ![](https://www.vedantu.com/question-sets/614c6cf7-e47e-4ea6-96b7-f39be984a9e31214625930411841977.png)

Answer 1

Here we will use the property of circle i.e, the angle subtended by an arc at the centre of the circle is twice the angle subtended by it on any other point on the circle to prove the given statement.

Complete step-by-step answer:
In the figure,
Let us first consider the arc XY.
The angle subtended by the arc XY at the centre P is $\angle XPY$ and the angle subtended at any other point on the circle is $\angle XZY$

Therefore, applying the following property of circle we get:-
The property is:-

The angle subtended by an arc at the centre of the circle is twice the angle subtended by it on any other point on the circle.

Hence on applying this property we get:-
$\angle XPY = 2\angle XZY.........................\left( 1 \right)$

Similarly, let us now consider the arc YZ.
The angle subtended by the arc YZ at the centre P is $\angle ZPY$ and the angle subtended at any other point on the circle is $\angle YXZ$

Therefore, applying the following property of circle we get:-
The property is:-

The angle subtended by an arc at the centre of the circle is twice the angle subtended by it on any other point on the circle.

Hence on applying this property we get:-
$\angle ZPY = 2\angle YXZ.........................\left( 2 \right)$
Now on adding equations 1 and 2 we get:-

$\angle XPY + \angle ZPY = 2\angle XZY + 2\angle YXZ$………………………………….(3)

Now from the figure it can be observed that:-

$\angle XPY + \angle ZPY = \angle XPZ$ ………………………………(4)

Putting the value from equation 4 in equation 3 we get:-

$$\angle XPZ = 2\angle XZY + 2\angle YXZ \\\ \Rightarrow \angle XPZ = 2(\angle XZY + \angle YXZ) \\\$$

Therefore, $LHS = RHS$

Hence Proved.

Note: Students should take note that the angle subtended by an arc, line segment, or any other section of a curve is one whose two rays pass through the endpoints of the arc.
Also the property used should be correct.