Question
Question: In the given figure, O is the centre of the circle. If \(\angle PBC = 25^\circ and \angle APB = 110^...
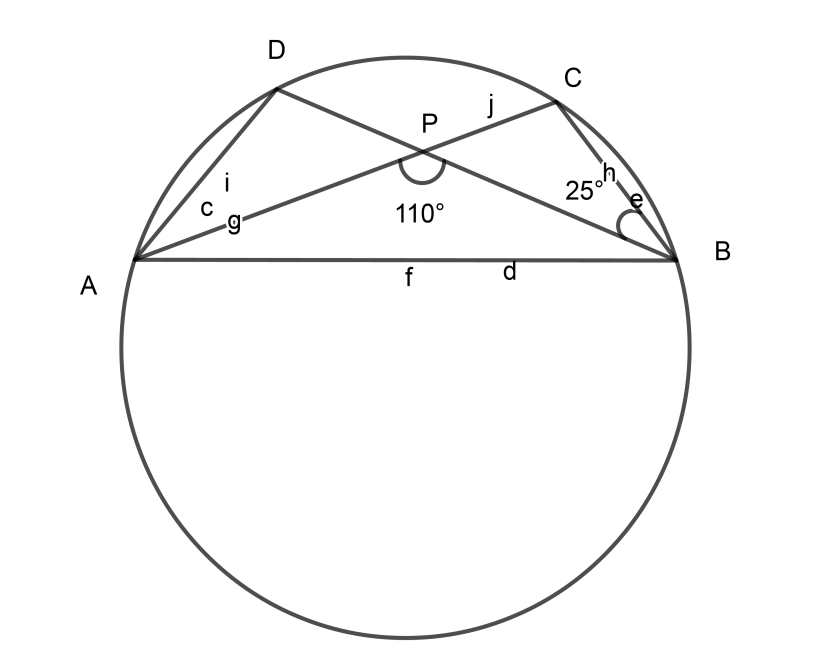
In the given figure, O is the centre of the circle. If ∠PBC=25∘and∠APB=110∘, find the value of ∠ADB
Solution
Hint: We can solve this problem by using the concept i.e.
Angles inscribed by same arc on the circumference of circle are always EQUAL
Complete step-by-step answer:
We will write the given first,
∠PBC=25∘and∠APB=110∘……………………………. (1)
To find the a∠ADB we should know the key concept given below,
Concept: Angles inscribed by same arc on the circumference of circle are always EQUAL
Therefore we can say Angles inscribed by arc AB are equal. That is,
∠ADB=∠ACB…………………………………. (2)
Now let’s find∠ACB,
As we all know ∠APC is a straight angle,
∠APC=180∘
But, ∠APCcan be written as,
∠APC=∠APB+∠CPB
∴180∘=110∘+∠CPB………………………….. [From (1)]
∴∠CPB=180∘−110∘
∴∠CPB=70∘……………………………….. (3)
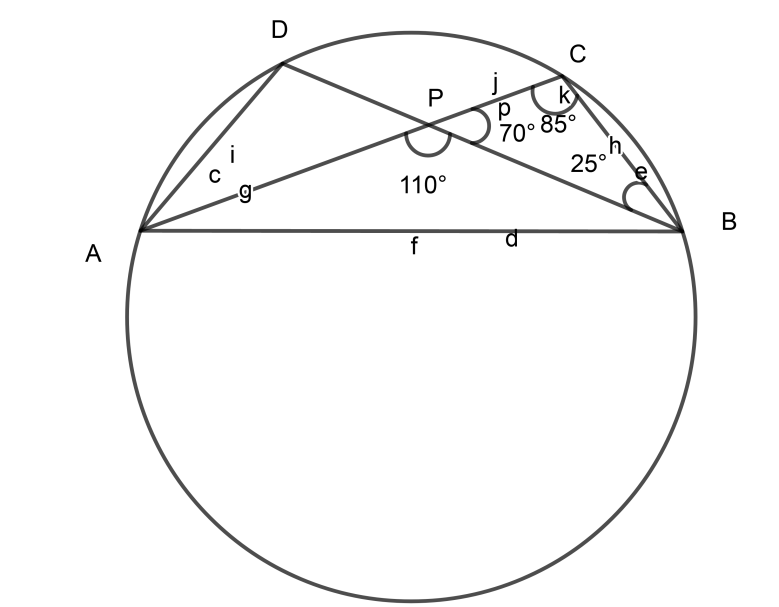
Now consider △BPC,
As the property of a triangle says that the sum of three angles of a triangle are 180∘,
∠CPB+∠PBC+∠BCP=180∘
∴70∘+25∘+∠BCP=180∘
∴∠BCP=180∘−95∘
∴∠BCP=85∘
We can write ∠BCP as ∠PCB
∴∠PCB=85∘
Now if we see the figure we will come to know that ∠PCB=∠ACB as P and A lie on the same line.
∴∠ACB=85∘
Our target is to find the ∠ADB therefore rewrite the equation (2)
∴∠ADB=∠ACB
Put the value of∠ACB=85∘,
∴∠ADB=85∘
Therefore the value of ∠ADB is 85∘.
Note: Always remember to draw diagrams for this type of problems to avoid confusion. Also, the property of a circle given by “Angles inscribed by the same arc on the circumference of a circle are always EQUAL” is very much important to solve this problem.
