Question

In the given figure, mass of man is $60\,Kg$ and the reading of weighing machine is $90\,Kg$ , the acceleration lift is:

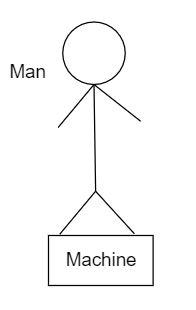
A) $\dfrac{g}{2}$ in upward direction
B) $g$ in upward direction
C) $\dfrac{g}{2}$ in downward direction
D) $g$ in downward direction

Answer 1

From the diagram given in the question, assume that the machine is upward lifting, then the equivalent forces are considered. From that find the value of the accelerating potential and whether it acts upward or downward by comparing the value of the true and the reading weight.

Useful formula:
The newton’s second law of motion is given by
$F = ma$
Where the $F$ is the force acting on the man, $m$ is the mass of the man and $a$ is the accelerating potential of the man.

Complete step by step solution:

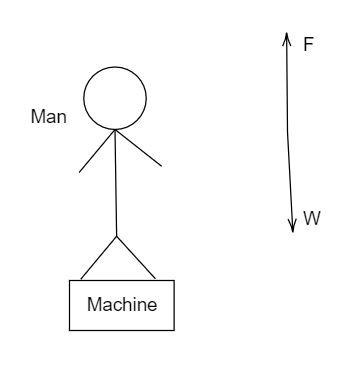
The true weight of the man, $w = 60\,Kg$
The reading weight of the man by the weighing machine, $W = 90\,Kg$
From the diagram it is clear that
$W = w + F$
Substitute the formula of the newton’s law of motion in the above step,
$W = w + ma$
The weight of the man is converted into the true mass by multiplying it with the gravity.
Substitute the value of the weight of the man and the reading of the weighing machine in the above step,
$90g = 60 + 60a$
Simplifying the above equation,
$60a = 30g$
By the further simplification,
$a = \dfrac{g}{2}$
The value of the reading provided by the machine is more than the true man weight. Hence the machine must be accelerated upward.

Thus the option (A) is correct.

Note: In case if the lift of the weighing machine acts downward, the reading shown by the machine as the weight of the man must be less when compared to that of the true weight of the man. In this case it is a downward lifting machine, it should show a weight less than the true weight of the man.