Question

In the given figure, ${m_A} = 2{\text{ }}kg$ and ${m_B} = 4{\text{ }}kg$. For what minimum value of $F, A$ starts slipping over $B$.

A. $24{\text{ }}N$
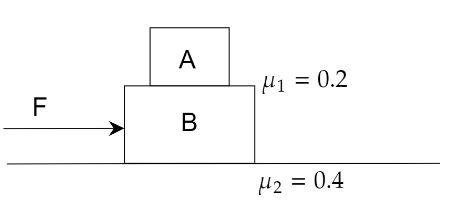
B. $36{\text{ }}N$
C. $12{\text{ }}N$
D. $20{\text{ }}N$

Answer 1

First of all, we have to find the frictional force between the block $B$ and the ground surface. Then, we have to find the frictional force between block $A$ and block $B$.By comparing the equations with that of force, we will find the value of $F$.

Complete step by step answer:

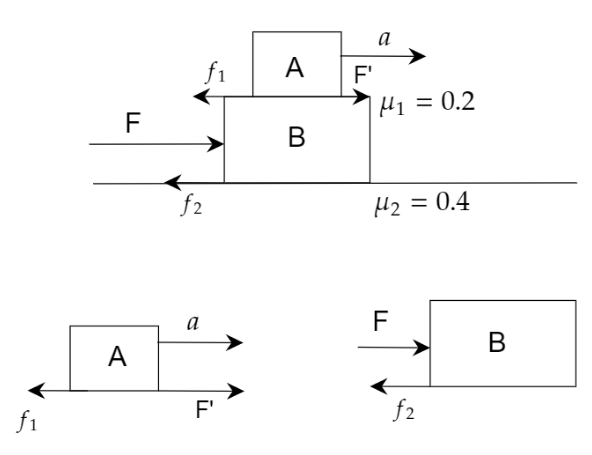
From the given diagram we will find the frictional forces,
The mass of block A, ${m_A} = 2{\text{ }}kg$
The mass of block B, ${m_B} = 4{\text{ }}kg$
${f_1} = {\mu _1}{m_A}g$
where ${f_1}$ is the frictional force that acts upon block A and block B, ${\mu _1} =$ coefficient of friction and $g =$ acceleration due to gravity.
Substituting all the values we get,
${f_1} = 0.2 \times 2 \times 10 = 4$

The frictional force between block A and B is $4{\text{ }}N$.As, the block just starts slipping then,
F’$= {f_1} = 4{\text{ }}N$
According to Newton’s Law we know,
F’$= {m_A} \times a$
where $a$ is the acceleration of the block.
Substituting the values we get,
$4 = 2 \times a$
$\Rightarrow a = 2$

Now, the frictional force between the block B and the ground,
${f_2} = {\mu _2} \times ({m_B} + {m_A}) \times g = 0.4 \times 6 \times 10 = 24$
Thus, the frictional force between block B and ground is ${\text{24 }}N$.
Again, using Newton’s Law for the whole system we get,
F$- {f_1} - {f_2} = {m_B} \times a$
Substituting all the values in the given question, we get,
F$- 4 - 24 = 4 \times 2$
$\therefore$F$= 36$
The minimum value of F so that the block $A$ just starts slipping is $36{\text{ }}N$.

So, the correct option is B.

Note: It must be noted that when a block starts to slip the frictional force always opposes the movement of the block. In order to oppose the movement of the block, the frictional force must be of the same magnitude as the force which causes motion but opposite in direction.