Question

In the given figure, if $PS = 14cm$ , then the value of $\tan \theta$ is equal to:

(A) $\dfrac{4}{3}$
(B) $\dfrac{{14}}{3}$
(C) $\dfrac{5}{3}$
(D) $\dfrac{{13}}{3}$

Answer 1

Hint : $\tan \theta$ is the ratio of perpendicular to the base. Observe the figure carefully to find the values of the perpendicular or the opposite side. And the base or the adjacent side. Then find their ratio to solve the question.

Complete step-by-step answer :
Observe the diagram

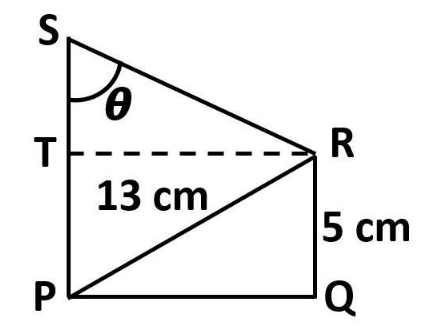
It is given in the question that,
$PS = 14cm$
From the diagram, we can observe that,
$PT = QR = 5cm$
And $PS = PT + TS$
$\Rightarrow 14 = 5 + TS$
Rearranging it we can write
$TS = 9cm$
Now, in $\Delta SRT$
We know that the trigonometric ratio of tan is the ratio of perpendicular to the base.
$\Rightarrow \tan \theta = \dfrac{{TR}}{{ST}}$ . . . (1)
In $\Delta PQR$ , from the diagram, and by Pythagoras theorem, we can observe that,
$P{R^2} = R{Q^2} + P{Q^2}$
By substituting the given values, we get
$\Rightarrow {13^2} = {5^2} + P{Q^2}$
Rearranging it we can write
$P{Q^2} = 169 - 25 = 144$
$\Rightarrow P{Q^2} = {12^2}$
$PQ = 12cm$
Now, from the diagram, we can observe that,
$PQ = TR = 12cm$
By substituting these values in equation (1), we can write
$\tan \theta = \dfrac{{12}}{9}$
$\Rightarrow \tan \theta = \dfrac{4}{3}$
Therefore, from the above explanation, the correct answer is, option (A) $\dfrac{4}{3}$
So, the correct answer is “Option A”.

Note : In this question, the most important part was observing the diagram carefully and understanding which side is equal, where will Pythagoras theorem be required etc. The solution was easy, difficult and an important part was how to reach the solution.