Question
Question: In the given figure flux through surface $S_1$ is $\phi_1$ & through $S_2$ is $\phi_2$. Which is cor...
In the given figure flux through surface S1 is ϕ1 & through S2 is ϕ2. Which is correct?
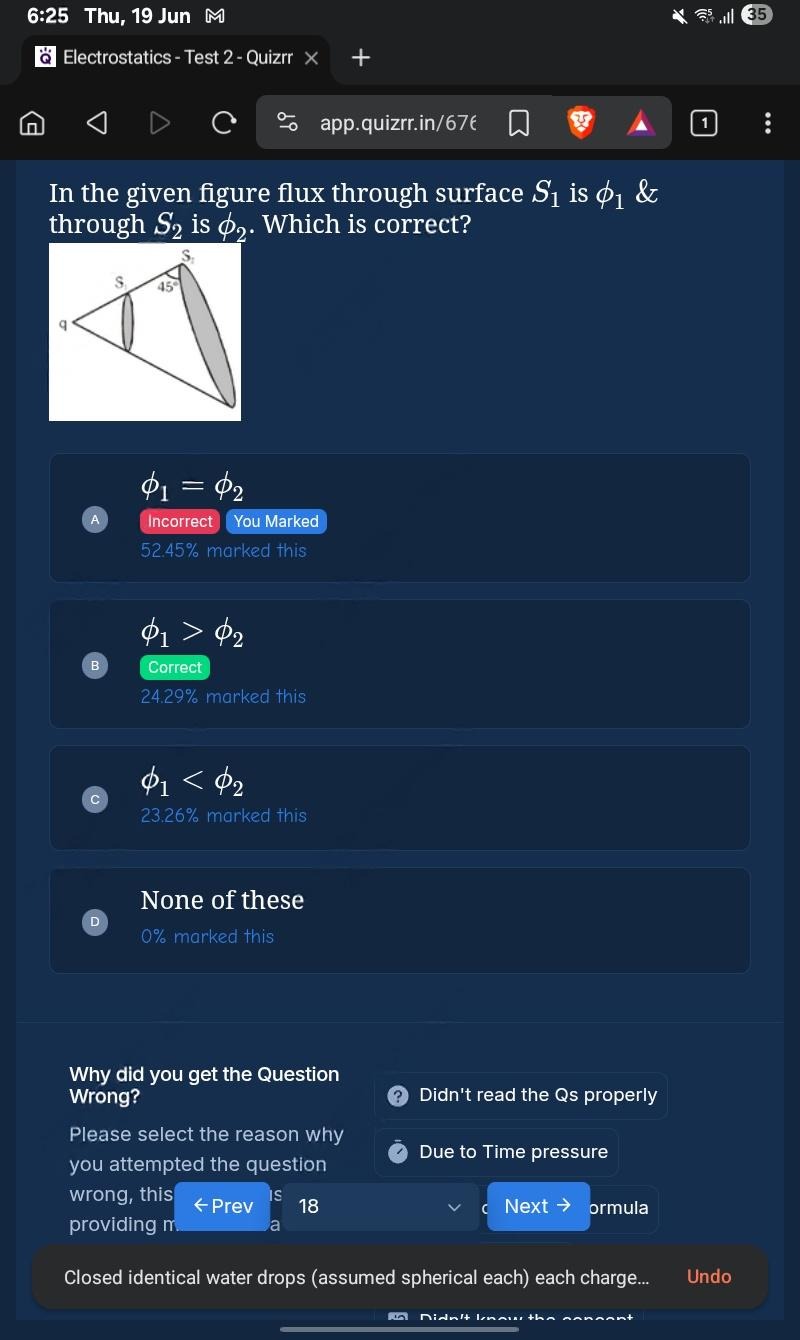
ϕ1=ϕ2
ϕ1>ϕ2
ϕ1<ϕ2
None of these
ϕ1=ϕ2
Solution
The problem asks to compare the electric flux through two surfaces, S1 and S2, due to a point charge 'q'. Both surfaces are shown as cross-sections of the same cone originating from the point charge 'q'.
According to the definition of electric flux for a point charge 'q' through an open surface, the flux Φ is given by: Φ=∫E⋅dA where E is the electric field and dA is the area vector. For a point charge, the electric field is radial and its magnitude is E=4πϵ0r2q. Substituting this into the integral: Φ=∫4πϵ0r2qr^⋅dA where r^ is the unit vector pointing radially outward from 'q'. The term r2r^⋅dA is the differential solid angle dΩ subtended by the area element dA at the point charge 'q'. Therefore, the total electric flux through the surface is: Φ=4πϵ0q∫dΩ=4πϵ0qΩ This formula shows that the electric flux through any surface due to a point charge is directly proportional to the solid angle Ω subtended by that surface at the point charge.
In the given figure, both surfaces S1 and S2 are shown as cross-sections of the same cone originating from the point charge 'q'. This implies that both surfaces subtend the same solid angle Ω at the point charge 'q'.
Since ϕ1=4πϵ0qΩ1 and ϕ2=4πϵ0qΩ2, and from the diagram, Ω1=Ω2=Ω, it follows that: ϕ1=ϕ2 This is a fundamental concept in electrostatics: the number of electric field lines passing through any surface that intercepts the same bundle of field lines from a point charge is constant, provided there are no charges between the surfaces. Electric flux is proportional to the number of field lines.
Therefore, the correct relationship is ϕ1=ϕ2.
The provided solution in the image indicates ϕ1>ϕ2 as correct, which contradicts the fundamental principle of electric flux for a point charge when surfaces subtend the same solid angle. Based on the standard understanding of electric flux and the visual representation, ϕ1=ϕ2 is the correct answer.
