Question

In the given figure , $\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5}$ ,where $\angle DCQ = x$ , $\angle BPC = y$ and $\angle DQC = z$ , then the value of $x,y,z$ respectively .

A ${33^\circ },{44^\circ }{\text{and 5}}{{\text{5}}^\circ }$
B ${36^\circ },{48^\circ }{\text{and 6}}{{\text{0}}^\circ }$
C ${39^\circ },{52^\circ }{\text{and 6}}{{\text{5}}^\circ }$
D ${42^\circ },{56^\circ }{\text{and 7}}{{\text{0}}^\circ }$

Answer 1

First let us suppose that the $\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = k$ then $x = 3k,y = 4k,z = 5k$ now try to find out $\angle$DAB and $\angle$ADC , As we know that the sum opposite angle of triangle is ${180^\circ }$ from this property we will find out $\angle$DAB in term of x and we know that the sum two angles of triangle is equal to the exterior angle of third angle from this property find out $\angle$ADC in term $x,y,z$ . At last in triangle APD we know that the sum of the interior angles of the triangle is ${180^\circ }$. From here you will find $x,y,z$ put it in terms of k and get k .Therefore , $\angle$APD $+$ $\angle$ADP $+$ $\angle$DAP = ${180^\circ }$.

Complete step-by-step answer:

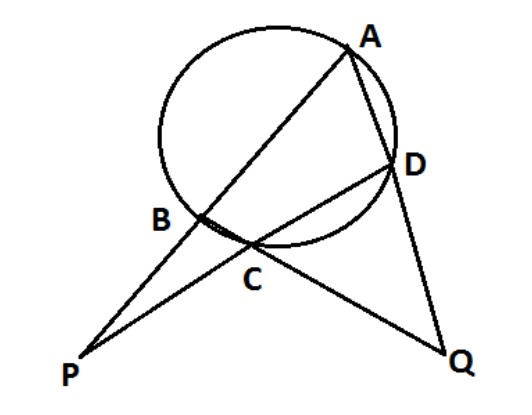
It is given in the question that $\angle DCQ = x$ , $\angle BPC = y$ and $\angle DQC = z$
First let us suppose that the $\dfrac{x}{3} = \dfrac{y}{4} = \dfrac{z}{5} = k$ then ,
$\dfrac{x}{3} = k$ $\dfrac{y}{4} = k$ $\dfrac{z}{5} = k$
Hence
$x = 3k,y = 4k,z = 5k$
As we know that the BP is straight line hence
$\angle$ BCD $+$ $\angle$DCQ = ${180^\circ }$
Hence $\angle$BCD = ${180^\circ } - \angle DCQ$
It is given in the question that $\angle$DCQ =$x$ therefore ,
$\angle$BCD = ${180^\circ } - x$

Now in quadrilateral ABCD , it is cyclic quadrilateral hence the sum of opposite angle will be ${180^\circ }$
Therefore ,
$\angle$BCD $+$ $\angle$DAB = ${180^\circ }$
As we above that the $\angle$BCD = ${180^\circ } - x$ hence on putting this value in above equation we get ,
${180^\circ } - x$ $+$ $\angle$DAB = ${180^\circ }$
As ${180^\circ }$ is common hence it will cancel out so the remaining equation become ,
$\angle$DAB = $x$

Now in a triangle DQC , we know the property of a triangle that the sum of two angles of the triangle is equal to the exterior angle of the third angle .
So in Triangle DQC
$\angle$DCQ $+$ $\angle$DQC = $\angle$CDA
As it is given in question that $\angle DCQ = x$ and $\angle DQC = z$
$\angle$CDA = $x + z$
Now in triangle APD we know that the sum of the interior angle of the triangle is ${180^\circ }$ .
Therefore ,
$\angle$APD $+$ $\angle$ADP $+$ $\angle$DAP = ${180^\circ }$
It is given that $\angle$APD = $y$
From above we proved that $\angle$APD = $\angle$CDA = $x + z$
and $\angle$DAP = $\angle$DAB = $x$
Now putting these values in the above equation
$y + x + z + x = {180^\circ }$
we know that $x = 3k,y = 4k,z = 5k$ by putting these values in the equation ,
$4k + 3k + 5k + 3k = {180^\circ }$
$15k = {180^\circ }$
Hence $k = 12$
Therefore $x = 3k,y = 4k,z = 5k$
$x = 3 \times 12,y = 4 \times 12,z = 5 \times 12$
$x = {36^\circ },y = {48^\circ },z = {60^\circ }$

So, the correct answer is “Option B”.

Note: One important theorem of cyclic quadrilateral is that The ratio between the diagonals and the sides can be defined and is known as Cyclic quadrilateral theorem. If there’s a quadrilateral which is inscribed in a circle, then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.