Question
Question: In the given figure, \(\angle AOB=90{}^\circ \) and \(\angle ABC=30{}^\circ \), Then \(\angle CAD=?\...
In the given figure, ∠AOB=90∘ and ∠ABC=30∘, Then ∠CAD=?
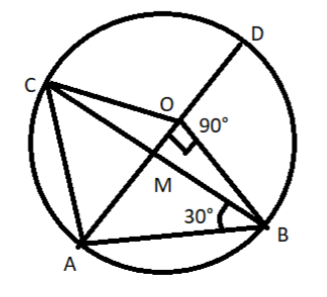
(a) 30∘
(b) 45∘
(c) 60∘
(d) 90∘
Solution
In triangle OAB, ∠OAB=∠OBA, calculate ∠OBA. Assume point “M” as shown in the diagram. ∠MBA=30∘(given). Find ∠MBC by subtracting ∠MBA from ∠OBA. As OC=OB=r. So, ∠OCM=∠OBM. Now calculate ∠COBand then calculate ∠CAO by using the fact that “angle subtended by a chord at the center of a circle is double of the angle subtended by the chord at any point lying on the circle.”
Complete step-by-step solution:
__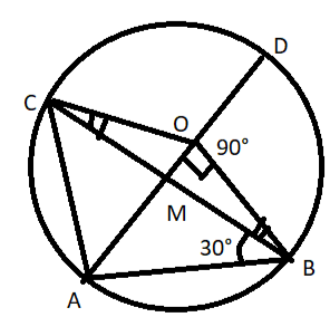
All the points are specified. Assume point of intersection of OA and BC on “M”.
In △OAB,OA=OB=radius of the circle.
We know that if two sides is a triangle are equal, their corresponding angles will also be equal.
i.e. ∠OAB=∠OBA
let ∠OAB=∠OBA=x
By angle sum property of a circle, sum of the angles of a △ is 180∘.
In △OAB-
∠OAB+∠OBA+∠AOB=180∘⇒x+x+90∘=180∘⇒2x=180∘−90∘⇒2x=90∘⇒x=45∘
So, ∠OBA=∠OAB=45∘
From diagram,
∠OBA=∠OBM+∠MBA⇒45∘=∠OBM+30∘⇒∠OBM=45∘−30∘⇒∠OBM=15∘
In △OCB
OC=OB (both are radius of the circle)
So, corresponding angles will also be equal in the △.
So, ∠OCB=∠OBC
We have calculated above that ∠OBM=15∘
⇒∠OBC=15∘ (see diagram)
So, ⇒∠OBC=∠OBM=15∘
Now, in △ OBM-
∠MOB=90∘(given)∠OBM=15∘(calculatedabove)
By angle sum property of triangle-
∠MOB+∠OBM+∠OMB=180∘90∘+15∘+∠OMB=180∘∠OMB=180∘−(90∘+15∘)∠OMB=75∘
By linear property straight lines on line BC-
∠CMO+∠OMB=180∘∠CMO+75∘=180∘[∠OMB=75∘,calculatedabove]∠CMO=180∘−75∘∠CMO=105∘
Now in △OCM−
∠OCM=15∘(calculatedabove)∠OMC=105∘(calculatedabove)
By angle sum property of a △
∠OCM+∠OMC+∠COM=180∘⇒15∘+105∘+∠COM=180∘⇒120∘+∠COM=180∘⇒∠COM=180∘−120∘⇒∠COM=60∘
From the diagram, we can see that
∠COB=∠COM+∠MOB∠COM=60∘(calcullatedabove)∠MOB=90∘(given)So,∠COB=60∘+90∘⇒∠COB=150∘
We know that the angle subtended by a chord of a circle at its center is double the angle subtended by the chord at any point on its circumference.
We can see the diagram that chord BC subtends ∠COB at the center of the circle and angle ∠CAB at the circumference.
So,
∠COB=2×∠CAB⇒150∘=2×∠CAB[∠COB=150∘ascalculatedabove]⇒∠CAB=2150∘=75∘
From the diagram, we can see that ∠CAB=∠CAD+∠OAB
∠CAB=75∘(calculatedabove)∠OAB=45∘(calculatedabove)
So,
75∘=∠CAO+45∘⇒∠CAD=75∘−45∘=30∘
Hence the required value of ∠CAD will be 30∘ and option (a) is the correct answer.
Note: We have used a theorem in the solution that the angle subtended by a chord at the center is double of the angle subtended by it on its circumference.
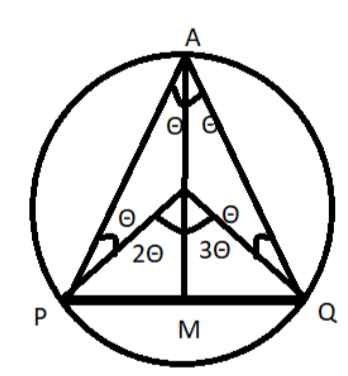
Given chord PQ of a circle subtending POQ at the centre O and PAQ at a point A n the circumference of the circle.
To prove:
∠POQ=2∠PAQ
Join AM such that AM is bisecting ∠PAQ
Let, ∠PAD=∠DAQ=θ
In △ADQ−OA=DQ(Bothequaltoradius)
So, corresponding angles will also be equal.
i.e. ∠OAQ=∠OQA
So, ∠OQA=θ
Now by exterior angle sum property- (in △AOQ−
∠OAQ+∠DQA=∠MOQ⇒θ+θ=∠MOq⇒∠MOQ=2θ
Similarly, in △APO− (exterior angles property)
∠POM=2θNoq,∠POQ=2θ+2θ=4θ(Seediagram)and∠PAQ=θ+θ=2
Hence, ∠POQ=2∠PAQ
