Question
Question: In the given figure \[\angle 1 = \angle 2\] and \[\Delta NSQ \cong \Delta MTR\], then prove that \[\...
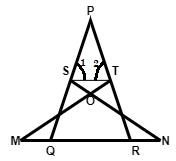
In the given figure ∠1=∠2 and ΔNSQ≅ΔMTR, then prove that ΔPTS∼ΔPRQ.
Solution
In the given question, we have to prove the similarity of two triangles (which means that the triangles are similar in shape, but not necessarily equal). For doing that we have to show that either of the three necessary conditions are true – two corresponding angles are equal (AA), two corresponding sides and the included angle is equal (SAS), or all the three sides are equal (SSS). Here, we have been given that two other triangles are congruent (which means that the two triangles are similar in shape and equal in too), so we can use that to show the similarity by showing the sides of the congruent triangles equal and using that to prove the equality of the triangles.
Complete step-by-step answer:
In the given question, we have been given:
∠1=∠2 and ΔNSQ≅ΔMTR
We have to prove:
ΔPTS∼ΔPRQ
Now, ΔNSQ≅ΔMTR
So, ∠NQS=∠MRT (cpct)
or, if we see the two angles from the point of view of the big triangle ΔPQR, we get:
\Rightarrow $$$$\angle PQR = \angle PRQ …(i)
Now, in ΔPST, we have:
∠1+∠2+∠SPT=180∘
Now, ∠1=∠2
So, ∠1+∠1+∠SPT=180∘
or, 2∠1+∠SPT=180∘ …(ii)
Now in ΔPQR, we have:
∠PQR+∠PRQ+∠QPR=180∘
Now, ∠PQR=∠PRQ (from (i))
So, ∠PQR+∠PQR+∠QPR=180∘
or, 2∠PQR+∠QPR=180∘
Now, ∠QPR=∠SPT (same angle)
So, 2∠PQR+∠SPT=180∘ …(iii)
Now, comparing equations (ii) and (iii), we have:
⇒ ∠1=∠PQR …(iv)
Now, in ΔPTS and ΔPRQ, we have:
⇒ ∠P=∠P (common angle)
⇒ ∠PST=∠PQR (from (iv))
Hence, ΔPTS∼ΔPRQ (AA similarity)
Hence, proved.
Note: So, we saw that in solving questions like these, we must first see what all has been given to us and write it down. Then, we need to write down what has been given to us. Then, we see if with what has been given to us, we can use some information or deduce some comprehensible information to prove what we need to prove. Like in this question, we used the information that sides of any two congruent triangles is equal and we then used this information to prove the similarity of the required two triangles. It is a point to note that if two triangles are congruent, then it is always true that they are similar too. But, if two triangles are only similar, then it is not always true that they are congruent too.
