Solveeit Logo
Login

Question

Question: In the given figure, after switch \(S\) is closed at time \[t = 0\], the emf of the source is automa...

In the given figure, after switch SS is closed at time t=0t = 0, the emf of the source is automatically adjusted to maintain a constant current i through S.
(a) Find the current through the inductor as a function of time.
(b) At what time is the current through the resistor equal to the current in the inductor?

Explanation

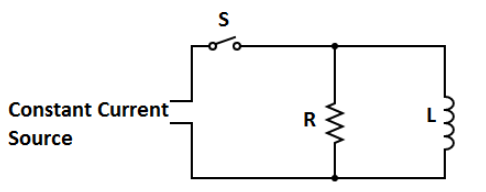
Solution

In the figure, we have a Resistor and inductor in the circuit and the current flowing through LR circuit is given as i=i0(1−e−RtL)i = {i_0}(1 - {e^{\dfrac{{ - Rt}}{L}}}) where i0=ER{i_0} = \dfrac{E}{R} which is called maximum current of the circuit, Junction rules we will find current in the inductor as a function of time.

Complete step by step answer:
(a) Let us suppose the current i1{i_1} flows in the resistor in downward direction and current i2{i_2} flows in the inductor in downward direction when the switch is closed at t=0t = 0. Total current through Current source says ii.Then we have,
i=i1+i2i = {i_1} + {i_2}
Now, the voltages across resistor is Ri1R{i_1} and voltage across inductor is given by,
−Ldi2dt- L\dfrac{{d{i_2}}}{{dt}}
So, Ri1−Ldi2dt=0R{i_1} - L\dfrac{{d{i_2}}}{{dt}} = 0
Ldi1dt+i1R=0L\dfrac{{d{i_1}}}{{dt}} + {i_1}R = 0
Above equation is similar to the general equation E=Ldidt+RiE = L\dfrac{{di}}{{dt}} + Ri
Whose solution is given by i=i0e−RtLi = {i_0}{e^{\dfrac{{ - Rt}}{L}}}
So we get the solution as,
i1=ie−RtL{i_1} = i{e^{\dfrac{{ - Rt}}{L}}}
Since, at t=0t = 0 i1=0{i_1} = 0 and maximum current is i0=i{i_0} = i
So we get,
i2=i−i1{i_2} = i - {i_1}
∴i2=i(1−e−RtL)\therefore {i_2} = i(1 - {e^{\dfrac{{ - Rt}}{L}}}) Which is the current through the inductor.

Hence, current through the inductor is given by i2=i(1−e−RtL){i_2} = i(1 - {e^{\dfrac{{ - Rt}}{L}}}).

(b) Since from part (i) we have,
i1=ie−RtL{i_1}= i{e^{\dfrac{{ - Rt}}{L}}}
⇒i2=i(1−e−RtL)\Rightarrow {i_2} = i(1 - {e^{\dfrac{{ - Rt}}{L}}})
Equate both equations we get,
(1−e−RtL)=e−RtL(1 - {e^{\dfrac{{ - Rt}}{L}}}) = {e^{\dfrac{{ - Rt}}{L}}}
Taking Natural logarithm on both sides:
(RtL)=ln⁡2(\dfrac{{Rt}}{L}) = \ln 2
∴t=LRln⁡2\therefore t = \dfrac{L}{R}\ln 2

Hence, the time at which current through inductor and resistor is t=LRln⁡2t = \dfrac{L}{R}\ln 2.

Note: Remember, when the switch is just closed the charges start to flow in the circuit as circuit gets completed and the inductor starts to build a magnetic field around it as the inductor reaches the maximum point of producing magnetic field it acts as a short circuit.The time at which inductor is fully charged is known as its time constant.