Question
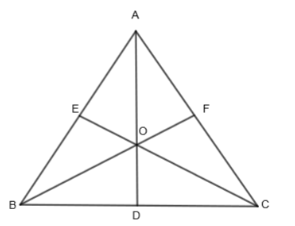
Question: In the given figure, AD, BF and CE are the medians of a triangle ABC and O is a point of concurrency...
In the given figure, AD, BF and CE are the medians of a triangle ABC and O is a point of concurrency of the medians. If AD = 6cm, then OD is equal to
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 32cm
Solution
Hint: In order to find the solution of this question, we will assume the length of OD as x and then we will apply the property of centroid that is the centroid divides the median in the ratio 2:1 and then we will be able to find the length of OD.
Complete step-by-step answer:
In this question, we have been asked to find out the length of OD when we have been given that AD, BF and CE are the medians of triangle ABC and O is the midpoint of the concurrency of the medians and AD = 6 cm.
To solve this question, we will first consider the length of OD as x cm. So, we can represent the triangle as,

Now, we know the property of centroid, that is, the centroid divides the median in the ratio of 2:1. So, we can say O divides the median AD is the ratio of 2:1, that is,
ODAO=12
Now, we have considered OD = x. So, we can write,
xAO=2
⇒AO=2x
Now, we know that the median AD can be represented as the sum of AO and OD. So, we can say,
AD = AO + OD
Now, we have been given that AD = 6cm and according to our considerations, we can say AO = 2x and OD = x. So, we can write,
6 = 2x + x
And we know that it can be further written as,
3x = 6
Now, we will divide the whole equation by 3. So, we get,
33x=36
x = 2
Now, we know that x = OD. So, we can say, OD = 2 cm.
Hence, we can say the length of OD is 2 cm.
Therefore, option (a) is the right answer.
Note: While solving the question, the possible mistake one can make is writing the property of the centroid wrong, that is, by writing the ratio 2:1 as 1:2 or 1:1 or something else which will definitely give us the wrong answer. Also, one can think of applying Pythagoras theorem but we haven’t been given any information regarding the type of the triangle. So, we cannot apply the Pythagoras theorem.
