Question
Question: In the given figure \(ABCD\) is a trapezium in which \(AB\parallel CD\) and \(AD=BC\) . Show that bo...
In the given figure ABCD is a trapezium in which AB∥CD and AD=BC . Show that both diagonal are equal, AC=BD .
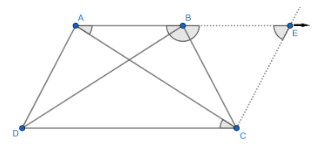
Solution
Hint: For solving this problem first we will prove that ∠DAB=∠CBA . Then we will prove two triangles congruent using side angle side congruence rule. Then, we will finally show that the diagonals of the given trapezium are equal.
Complete step by step answer:
Given:
We have trapezium ABCD in which AB∥CD and AD=BC .
Construction: Draw a line parallel to AD through C and extend the segment AB to meet the line drawn through C . Let they intersect at a point E .
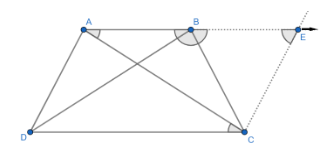
Now, as it is given that AB∥CD so AE∥CD and by construction, we can say that AD∥CE . Then, AECD is a quadrilateral in which opposite sides are parallel so, AECD will be a parallelogram. Then, AD=CE as opposite sides of the parallelogram are equal.
Now, consider ΔBCE we can write that, AD=BC=CE . So, the ΔBCE is an isosceles triangle in which BC=CE . As we know that in an isosceles triangle angles opposite to equal sides of an isosceles triangle are equal. Then,
∠CBE=∠CEB.........(1)
Now, as by construction AE∥CD and AE in the transversal then, interior angles on the same side of the transversal are supplementary angles. Then,
∠DAB+∠CEB=1800⇒∠DAB=1800−∠CEB
Now, using the equation in the above equation. Then,
∠DAB=1800−∠CEB⇒∠DAB=1800−∠CBE...............(2)
Now, as AE is a straight line, so ∠CBA and ∠CBE will be linear pairs. Then,
∠CBA+∠CBE=1800⇒∠CBA=1800−∠CBE............(3)
Now, comparing equation (2) and equation (3). Then,
∠DAB=1800−∠CBE=∠CBA⇒∠DAB=∠CBA..............(4)
Now, consider ΔABD and ΔBAC . Then,
AB=BA (common)∠DAB=∠CBA (from 4)AD=BC (Given)
Now, by the side angle side congruence rule we can write that ΔABD≅ΔBAC . And as we know that in a pair of congruent triangles corresponding sides of the triangle are equal. Then, AD=BC .
Thus, we have proved that diagonals of the given trapezium are equal in length.
Hence, proved.
Note: Here, the student must take care of the geometrical properties of the parallelogram. Moreover, be careful in writing the name of congruent triangles. For example in this question we cannot write that ΔADB≅ΔBAC , the correct way is ΔABD≅ΔBAC .
