Question
Question: In the given figure, ABCD is a square, BCF is an equilateral triangle and AEDF is a rhombus. Find \(...
In the given figure, ABCD is a square, BCF is an equilateral triangle and AEDF is a rhombus. Find ∠EAF
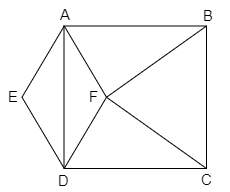
A. 30∘
B. 120∘
C. 150∘
D. None of these
Solution
From the figure, it is shown that ∠AFB and ∠CFD are right angles. As BCF is an equilateral triangle, so calculate ∠BFC. As we know that angles around a point add up to 360∘. From this find the value of ∠AFD. From the properties of the rhombus, the sum of adjacent angles of the rhombus is supplementary. From this property, we will get the value of ∠EAF.
Complete step by step answer:
From the figure, it is clear that ∠AFB and ∠CFD is right angles. So,
⇒∠AFB=∠CFD=90∘
As BCF is an equilateral triangle, we know that all angles of an equilateral triangle are equal. Then,
⇒∠BFC=60∘
Now, we know that all angles around a point add up to 360∘. Thus at point F,
⇒∠BFC+∠AFB+∠AFD+∠CFD=360∘
Substitute the values,
⇒60∘+90∘+∠AFD+90∘=360∘
Add the terms on the left side,
⇒240∘+∠AFD=360∘
Move the angle value on the right side,
⇒∠AFD=360∘−240∘
Subtract the value on the right side,
⇒∠AFD=120∘
Now, apply the property of rhombus states that the sum of adjacent angles of a rhombus is supplementary. So,
⇒∠AFD+∠EAF=180∘
Substitute the value,
⇒120∘+∠EAF=180∘
Move the angle value on the right side,
⇒∠EAF=180∘−120∘
Subtract the value on the right side,
⇒∠EAF=60∘
Thus, the value of ∠EAF is 60∘.
Hence, option (D) is the correct answer.
Note: A square is a quadrilateral in which all the four sides are equal in length and all the angles are equal. All the angles are equal to 90 degrees i.e. they are right angles.
A rhombus is a type of quadrilateral in which all four sides are of equal length. Also, the diagonals are perpendicular to one another and bisect each other too.
A triangle whose all three sides are of equal length is called an equilateral triangle. The measure of each angle of a triangle is 60 degrees.
