Question
Question: In the given figure ABCD is a quadrilateral in which AB = AD. The bisector of \(\angle \)BAC and \(\...
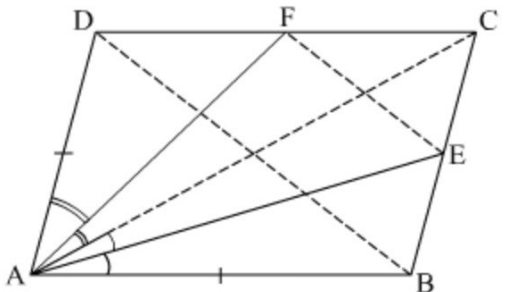
In the given figure ABCD is a quadrilateral in which AB = AD. The bisector of ∠BAC and ∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.
Solution
Hint: First, join AC, BD and EF. Now, in triangle CAB, AE is the bisector of ∠BAC. Use the angle bisector theorem to get ABAC=BECE. Similarly, from triangle CAD, you get ADAC=DFCF. Substitute AB = AD to get ABAC=DFCF. Equate the previous equation with this one to get EBCE=FDCF. Now, use the converse of Intercept Theorem to get the final answer.
Complete step by step answer:
In this question, we are given that ABCD is a quadrilateral in which AB = AD. The bisector of ∠BAC and∠CAD intersect the sides BC and CD at the points E and F respectively.
We need to prove that EF || BD.
Construction: Join AC, BD and EF.
In triangle CAB, AE is the bisector of ∠BAC.
Now, we will use the angle bisector theorem on triangle CAB.
The Angle Bisector Theorem says that an angle bisector of a triangle will divide the opposite side into two segments that are proportional to the other two sides of the triangle.
Using the above theorem, we will get the following:
ABAC=BECE …(1)
Similarly, in triangle CAD, AE is the bisector of ∠DAC.
Now, we will use the angle bisector theorem on triangle CAB.
Using the angle bisector theorem, we will get the following:
ADAC=DFCF
Now, we are given that AB = AD. Substituting this in the above equation, we will get the following:
ABAC=DFCF …(2)
From equations (1) and (2), we will get the following:
EBCE=FDCF
Thus, in triangle CBD, E and F divide the sides CB and CD respectively in the same ratio. Therefore, by the converse of Intercept Theorem, we have EF ∣∣ BD.
Hence proved.
Note: In this question, it is very important to know the angle bisector theorem. It is also important to know the intercept theorem. The intercept theorem states if a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.
