Question

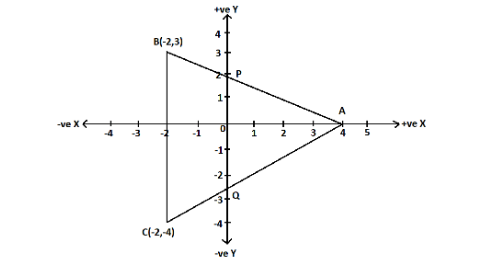
In the given figure ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
(i) Write the coordinates of A.
(ii) Find the length of AB and AC.
(iii) Find the ratio in which Q divides AC.
(iv) Find the equation of the line AC.

Answer 1

Hint : We can clearly see where the point A is, So note down its coordinates from the diagram. Find the length of AB and AC using distance between two points formula which is mentioned below. The ratio in which Q divides AC can also be calculated using the below mentioned formula. Equation of Ac is found by using two points form a line equation.
1. Distance between two points $A\left( {{x_1},{y_1}} \right)$ and $B\left( {{x_2},{y_2}} \right)$ is $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_2}} \right)}^2}}$
2. If a point P divides a line in the ratio m:n, then its coordinates will be $\left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$ , where $A\left( {{x_1},{y_1}} \right)$ and $B\left( {{x_2},{y_2}} \right)$ are the end points on the line.
3. Two points form of a line equation is $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$ , where $A\left( {{x_1},{y_1}} \right)$ and $B\left( {{x_2},{y_2}} \right)$ are the two points.

Complete step-by-step answer :
We are given that ABC is a triangle and BC is parallel to the y-axis.
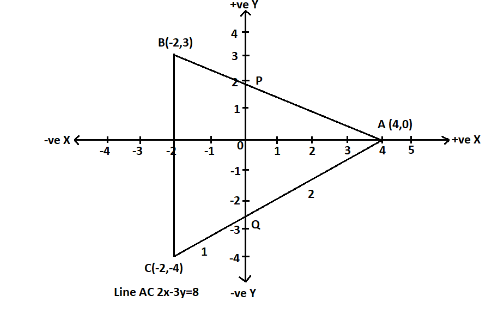
(i) Coordinates of A is $\left( {4,0} \right)$ , as the point A is on the x-axis, its y-coordinate will be zero.
So, the correct answer is “ {4,0}”.

(ii) Length of AB and AC
In AB, $\left( {{x_1},{y_1}} \right) = A\left( {4,0} \right),\left( {{x_2},{y_2}} \right) = B\left( { - 2,3} \right)$
Length of AB is $\sqrt {{{\left( { - 2 - 4} \right)}^2} + {{\left( {3 - 0} \right)}^2}} = \sqrt {36 + 9} = \sqrt {45} = 3\sqrt 5$ units.
In AC, $\left( {{x_1},{y_1}} \right) = A\left( {4,0} \right),\left( {{x_2},{y_2}} \right) = C\left( { - 2, - 4} \right)$
Length of AC is $\sqrt {{{\left( { - 2 - 4} \right)}^2} + {{\left( { - 4 - 0} \right)}^2}} = \sqrt {36 + 16} = \sqrt {52} = 2\sqrt {13}$ units.
So, the correct answer is “$2\sqrt {13}$ units”.

(iii) Ratio in which Q divides AC.
Here Ratio is m:n and $\left( {{x_1},{y_1}} \right) = A\left( {4,0} \right),\left( {{x_2},{y_2}} \right) = C\left( { - 2, - 4} \right)$
As we can see, Q is on the y-axis, so its x-coordinate will be zero.
Therefore, the coordinates of Q is $\left( {0,y} \right)$ which are equal to $\left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$
Corresponding coordinates are equal.
Therefore, $0 = \dfrac{{m{x_2} + n{x_1}}}{{m + n}}$
$\Rightarrow m{x_2} + n{x_1} = 0\left( {m + n} \right) = 0$
$\Rightarrow m{x_2} = - n{x_1}$
$\Rightarrow m\left( { - 2} \right) = - n\left( 4 \right)$
$\Rightarrow - 2m = - 4n$
$\therefore \dfrac{m}{n} = \dfrac{{ - 4}}{{ - 2}} = \dfrac{2}{1}$
Therefore, Q divides AC in the ratio 2:1.
So, the correct answer is “2:1”.

(iv) Equation of line AC.
Here the two points are $\left( {{x_1},{y_1}} \right) = A\left( {4,0} \right),\left( {{x_2},{y_2}} \right) = C\left( { - 2, - 4} \right)$
Two points form of a line equation is $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$
This gives, $y - 0 = \dfrac{{ - 4 - 0}}{{ - 2 - 4}}\left( {x - 4} \right)$
$\Rightarrow y = \dfrac{{ - 4}}{{ - 6}}\left( {x - 4} \right)$
$\Rightarrow 6y = 4\left( {x - 4} \right)$
$\Rightarrow 6y = 4x - 16$
$\Rightarrow 4x - 6y = 16$
$\therefore 2x - 3y = 8$
The equation of line AC is $2x - 3y = 8$ .
So, the correct answer is “ $2x - 3y = 8$”.

Note : Distance is a measurement, so it will always have units. If units are not mentioned in the question, you can just put the word “units” after the distance value. When two points are given, we can also find the line equation by finding the slope of the line and then using the slope-point form.