Solveeit Logo
Login

Question

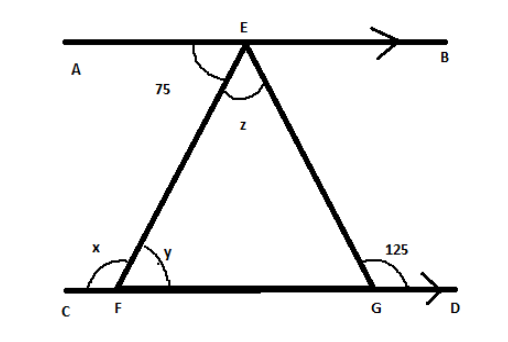
Question: In the given figure, AB\(||\)CD. Find in degree the value of \(x - y + z\) (Input the value without ...

In the given figure, AB∣∣||CD. Find in degree the value of x−y+zx - y + z (Input the value without degree).

Explanation

Solution

Here in this question properties of parallel lines and interior angle property of a triangle will get used. By this we can find the values of x, y and z
Properties of parallel lines: Here AB is parallel to CD and EF and EG are intersecting lines. . In this question the following properties will get used.

  1. Alternate angles are equal (∠AEF&y∘)(\angle AEF \& {y^ \circ })
  2. Interior sum of angles on the same side of transverse line (75∘{75^ \circ }+x∘{x^ \circ }=180∘{180^ \circ })
  3. Property of triangle: Sum of interior angles of triangle is 180∘{180^ \circ } (triangle EFG)

Complete step by step solution:
In the given figure AB||CD , EF is an intersecting line so here we will first apply interior angle property also known as complementary angles.
75∘+x∘=180∘{75^ \circ } + {x^ \circ } = {180^ \circ } (Complementary angles)
x∘=105∘{x^ \circ } = {105^ \circ }
Now for finding y˚ apply alternate angle property therefore angle ∠AEF=y∘\angle AEF = {y^ \circ }
y∘=75∘=∠EFG{y^ \circ } = {75^ \circ } = \angle EFG
Now to find the value of z˚ we have to use the angle sum property of a triangle.
Here ∠FEG+∠EFG+∠EGF=180∘\angle FEG + \angle EFG + \angle EGF = {180^ \circ } ................equation 1.
Now, ∠EGD+∠EGF=180∘\angle EGD + \angle EGF = {180^ \circ } (Sum of angles on a straight line is180∘{180^ \circ })
125∘+∠EGF=180∘{125^ \circ } + \angle EGF = {180^ \circ }
∠EGF=55∘\angle EGF = {55^ \circ }
Now putting values of∠EFG\angle EFG, ∠EGF\angle EGF in equation 1, we will get ∠FEG\angle FEG
∠FEG+75∘+55∘=180∘\angle FEG + {75^ \circ } + {55^ \circ } = {180^ \circ }
∠FEG=50∘\angle FEG = {50^ \circ } (Which is z∘{z^ \circ }), therefore z∘=50∘{z^ \circ } = {50^ \circ }

{x^ \circ } - {y^ \circ } + {z^ \circ } = {105^ \circ } - {75^ \circ } + {50^ \circ }\\\
x∘−y∘+z∘=80∘{x^ \circ } - {y^ \circ } + {z^ \circ } = {80^ \circ }

Note:
1. We have applied properties of parallel line on intersecting line EF but we can also apply these same properties on intersecting line EG.
2. Angle properties can be confusing sometimes so students should not be confused between alternate angles and corresponding angles.
3. Don’t forget to mark degrees on the angles.