Question
Question: In the given figure a string of linear mass density m and length L is stretched by a force \[F=(Fo-k...
In the given figure a string of linear mass density m and length L is stretched by a force F=(Fo−kt)N where Fo & k are constant and t is time t = 0, a pulse is generated at the end P of the string. As the pulse reaches the point Q, the force vanishes. The value of K in the above equation is
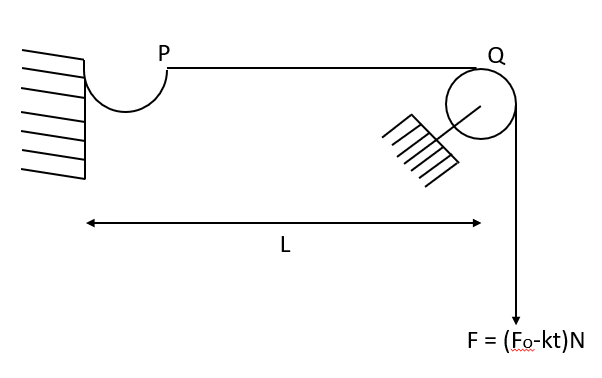
Solution
Firstly, we will find the value of the time for the pulse to reach the end Q of the string by putting F=0 in the given expression for the force F=F0−kt.Then, using the formula for the velocity of wave in a stretched string, that is V=mT . We can find the expression for the velocity of the pulse. Finally, substituting v=dtdxand integrating the resulting expression, we will get the required value of the constant k.
Formula Used: V=mT
Where T is Tension, V is Velocity and m is linear mass density of the string.
Complete step-by-step solution:
Tension in the string is, T=F0−kt
et the velocity of pulse in the string is 'V' and the time take by the pulse to travel distance from P to Q is t0. Then at time t0,
0=F0
0=F0−kt0
Hence,t0=KF0
Now, V=mT
Therefore, dtdx=mF0kt
∫0Ldx=m1∫0t0(F0−kt)1/2dt
L=m1×3k−2[(F0−kt)3/2]0t0
L=3km−2[0−F03/2]
K=3Lm2F03/2
After solving. We get value ofK=3L2mF03
Hence, the value of K in the equation F=(Fo−kt)N is K=3L2mF03
Note: Since, velocity 'V' is not constant with time as it is Varying with time. Also, time is not being calculated along with the pulse by speeddistance formula because velocity ‘V’ is not constant. That’s why we are using V=mT .After Integration, we will get the value of k.
