Question

In the given figure a semicircle is drawn with the centre O as centre and AB as diameter. Semicircles are drawn with AO and BO as diameter. If AB $=$ 28 cm, find the perimeter of the shaded region.

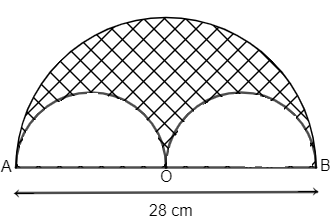
A.98 cm
B.48 cm
C.80 cm
D.88 cm

Answer 1

Hint: Perimeter of circle i.e. circumference of a circle is given as $2\pi r$, where r is the radius of the circle, and value of $\pi$ is $\dfrac{22}{7}$. Perimeter is defined as the sum of the path of that curve. Diameter is given as twice the radius of any circle. Use these concepts to solve the given problem.

Complete step by step answer:

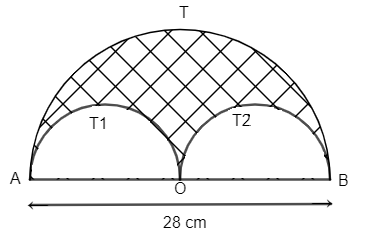
So, we need to find the perimeter of the shaded region. And as we know the perimeter of any curve is the length of the path of that curve. It means we need to add the path length of the shaded region i.e. length of the Arc ATB $+$ length of Arc $A{{T}_{1}}O$ $+$ length of Arc $O{{T}_{2}}B$.
As we know the diameter of the larger semicircle is 28 cm and hence the diameter of smaller semicircle will be $\dfrac{28}{2}=14cm$
Now, we know the circumference/ perimeter of any full circle is $2\pi r$ , where r is the radius of that circle.
It means the perimeter of the curve part of the semi-circle (leaving diameter) is given as $\dfrac{2\pi r}{2}=\pi r$ .
Now, as we have perimeter of shaded region as
Perimeter of shaded region $=$ Arc ATB $+$ Arc $A{{T}_{1}}O$ $+$ Arc $O{{T}_{2}}B$
Hence, radius of larger semicircle $=\dfrac{diameter}{2}$
$=\dfrac{28}{2}=14cm$
And radius of smaller semi-circle $=\dfrac{diameter}{2}$
$=\dfrac{14}{2}=7cm$
Hence, we can write the perimeter of shaded region as
$=\pi \times$ radius of larger semi-circle $+2\pi \times$ radius of smaller semi-circle
$=\pi \times 14+2\pi \times 7$
$=14\pi +14\pi$
$=28\pi$
So, perimeter of shaded region $=28\pi$
We know the value of $\pi$ is $\dfrac{22}{7}$
So, we get perimeter of shaded region $=28\times \dfrac{22}{7}$
$=4\times 22$
$=88cm$
Hence, option (D) is the correct answer.

Note: Don’t consider the diameter of the larger semi-circle in the calculation of the perimeter of it or with the shaded region as well. So, be clear with the definition of perimeter and involve only the path of the shaded region. Don’t use any other length to get the perimeter.Be clear with the formula of circumference and area of circle. Area is given as $\pi {{r}^{2}}$ and circumference is given as $2\pi r$. Don’t use the formulae in a reverse manner, it is the general confusion among the students.