Question
Question: In the given figure a constant force \[\overrightarrow {{F_a}} \] of magnitude \[82.0\;{\text{N}}\] ...
In the given figure a constant force Fa of magnitude 82.0N is applied to a 3.00kg shoe box at angle θ=53.00 causing the box to move up a frictionless ramp at constant speed. How much work is done on the box by Fa when the box has moved through vertical distance h=0.150m?
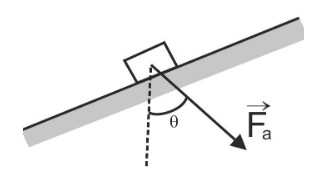
Solution
In this question, the concept of the conservation of the energy will be used, that is the total energy of the system remains constant. Here, the speed of the box is constant means there is no change in the Kinetic Energy so the change in the potential Energy is equal to the amount of work done.
Complete step by step answer:
In this question, firstly we consider the fact that there is no change in Kinetic Energy when the applied force Fa causes the box to move up a frictionless ramp at a constant speed. As because the definition of Kinetic Energy says that there is no change in Kinetic Energy when a Force is applied in a frictionless surface:
⇒ΔK=0
Where, ΔK is the change in Kinetic Energy.
Thus, in the above scenario, the work done by F1 must be equal to the negative work done by the gravity.
So, according to the above statement,
⇒Wa=−Wg
Where, Wais the work done on the box and Wg is the work done by gravity.
Since the box is displaced vertically upward so work done on the box is given by
Wa=mgh
Here, the mass of the box is m, the height is h, and the acceleration due to gravity is g.
Now we putting the values as given in the question we get m=3.00kg,g=9.80m/s2, h=0.150m
So, we have,
⇒Wa=(3)(9.80)(0.150)
After simplification we get,
∴Wa=4.41J
So, the correct answer is 4.41J.
Note: It should be kept in mind that if an inclined plane is frictionless and force is applied to move an object, the Kinetic Energy is zero. If any value is considered, the whole problem will go wrong. Facts of negative work done should be kept in mind while solving the last part of the problem. When an object is displaced vertically upward, regardless of negative work done, we should consider it positive while solving with values.
