Question
Question: In the given figure, \(a = 15m/{s^2}\) represents the total acceleration of a particle moving in the...
In the given figure, a=15m/s2 represents the total acceleration of a particle moving in the clockwise direction in a circle of radius R=2.5m at a given instant of time. The speed of the particle is:
A.6.2m/s
B.4.5m/s
C.5.0m/s
D.5.7m/s
Solution
Hint: The net acceleration given is the vector sum of its tangential acceleration arising due to angular acceleration and its centripetal acceleration, which acts radially inward. The centripetal acceleration is dependent on the speed of the particle as: ac=rv2
Complete step by step answer:
A particle in circular motion could be under the action of two forces. One force necessary to keep it rotating with a speed, which is called the centripetal force and the other tangential force, which could change the speed of rotation of the body.
The centripetal force acts towards the centre and is given by the relation :
Fc=rmv2
The tangential force acts tangential to the circle and can be given as :
Ft=dtdvt=dtd(rω)If both these forces act on a body, the net force and acceleration can be found by taking the vector sum of the two forces.
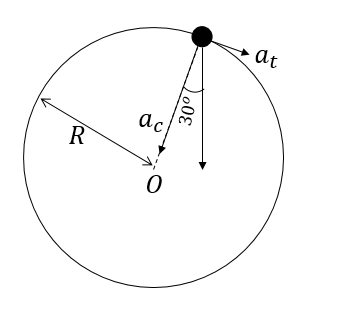
Here, the net acceleration at the point is given to make an angle of 30o with the radius.
We can find the component of this Net acceleration along the radius:
ar=anetcos(30)=15×23
Now, we know this is the centripetal acceleration of the body. So let us use equation (1) to find the speed of the particle.
The centripetal acceleration would be : ac=mFc=rv2
So rv2=1523
v2=2.5×1523=32.4375m/s
v=5.695m/s≈5.7m/s
Thus, the required answer is option D.
Additional information:
Similar to the centripetal force, there exists a counterforce called the centrifugal force. This force is experienced by particles that lie on a rotating body. Like a person inside a turning car. This force is not due to any push or pull but due to inertia. The person inside the car tends to move tangentially. But when the car gets a centripetal force and turns, The frame of reference of the person rotates and this makes him feel the opposite force. The value of this force would be exactly opposite as that of centripetal force and acts outward from along the radius.
Note: Note that the velocity we obtained is the velocity for that particular point. The next instant, this velocity changes. Also, since the centripetal acceleration is always along the radial direction and the tangential acceleration perpendicular to it, The magnitude and direction of acceleration also changes every instant.
