Question

In the given distribution of electric field lines, how is the electric field at X related to the electric field at Y?

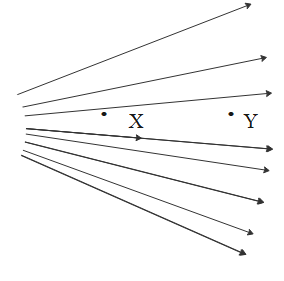
A. ${{E}_{x}}<{{E}_{y}}$
B. ${{E}_{x}}={{E}_{y}}$
C. ${{E}_{x}}>{{E}_{y}}$
D. ${{E}_{x}}.{{E}_{y}}=1$

Answer 1

The relative density of magnetic field lines around a point corresponds to the relative magnitude of electric field at that point. In other words, if electric field lines around a point X are denser than electric field lines at another point Y. Then, the electric field is stronger at point X as compared to electric field at point Y.

Complete step-by-step answer:
Faraday introduced the concept of field lines for visualizing electric fields around charge configurations geometrically. Faraday called them lines of force. An electric field line is defined as a curve, the tangent to each point of which gives direction of the net electric field at that point.

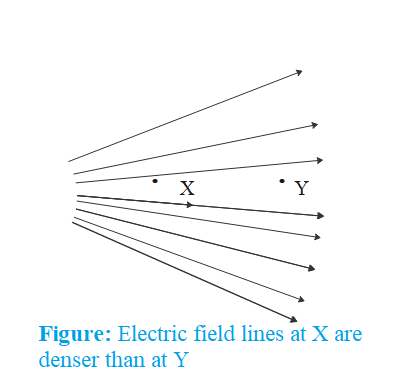
The relative density of electric field lines around a point corresponds to the relative magnitude of electric field at that point.
Since, electric field lines around point Y are less dense than electric field lines around point X. Therefore, electric field at X is stronger relatively i.e. magnitude of electric field at X is greater than magnitude of electric field at Y or ${{E}_{x}}>{{E}_{y}}$
So, the correct answer is “Option C”.

Additional Information: The field lines never intersect each other because if they do so then, at the point of intersection, there must be two directions of electric field which is not possible.
The electric field lines are always perpendicular to equipotential surfaces.

Note: Electric field lines are always directed away from a positive charge and towards a negative charge.
To compare the electric field at two points, it is not the density of electric field lines that is important. It is the relative density that helps us compare electric fields at two points.